Many investment organizations continue to benchmark their funds’ performance against the classic 60/40 mix of domestic stocks and bonds. This posture limits their ability to earn superior risk-adjusted returns. The authors argue that investors can fully realize the well-established benefits of asset class diversification only if they are seriously willing to revisit their policy portfolios, investment guidelines, and benchmarks. 

Academic researchers have started to examine the interaction of value and momentum signals across asset classes in levered long–short investment programs. The authors go beyond the existing literature by studying the empirical risk-and-return dynamics of carry, value, and momentum exposures across a wide range of asset classes in the long-only setting in which institutional investors actually implement global tactical asset allocation (GTAA) strategies.

Using a simple portfolio construction methodology to mitigate the likelihood of data mining, the authors compare three strategies over the 37-year period from 1980 to 2016: a two-asset US universe, a four-asset global universe, and a 15-asset-class diversified universe. Their main finding is that an investor with an active risk budget of 2% could have relied on carry, value, and momentum to drive economically significant excess returns in an unlevered portfolio as long as the opportunity set of asset classes was broad enough. In the diversified universe, the annual risk-adjusted alpha is 122 basis points (bps) and volatility is 184 bps, for an active information ratio of 0.67. By contrast, in the more restricted US and global universes, the annual risk-adjusted alpha produces information ratios of 0.13 and 0.18, respectively.  

Yet the investor can realize the benefits of such broad diversification only if the fund’s investment guidelines permit positions in the additional asset classes. Furthermore, the policy must allow symmetric bets for and against these markets. In a long-only portfolio, these bets will take the form of overweights and underweights, so the policy portfolio or benchmark must include all the permissible asset classes. For the purpose of the simple exercise set forth in this article, the authors use an equal-weighted benchmark. They find that “surprisingly simple models can add surprisingly large excess returns with surprisingly modest asset allocation ‘bets’ when applied across a sufficiently diverse array of asset classes.”

The data set used in this study encompasses return, yield, earnings, and corporate default and recovery rates for 15 asset classes including fixed income, commodities, real estate investment trusts (REITs), and equity investments. The analysis begins on January 1, 1980, and extends through December 31, 2016. The authors define carry as the expected return of an asset class under the assumption that its valuation will remain constant. Value assumes that prices will revert toward normalized historical averages, and momentum is the continuation of stock prices moving higher or lower. The article presents a detailed explanation of the specific measures employed to quantify the return drivers; in general, those measures take asset class differences into account while reflecting the authors’ preferences for simplicity and actual practice. In brief, the authors build three signals for each asset class:

• Carry = yield + growth; growth is specific to each asset class.
• Value = negative of the trailing five-year annualized return.
• Momentum = trailing one-year return.

The authors construct carry, value, and momentum strategy portfolios for the US universe, containing domestic stocks and bonds; the global universe, containing US and developed ex US stocks and bonds; and the diversified universe, containing 15 asset classes; the asset classes were added as return data for them became available over the course of the study period. For example, in January 1992 the number of asset classes rose from 11 to 12 when data for leveraged loans became available. The benchmark for each strategy is the equal-weighted portfolio, that is, the benchmark weight for each asset class is 1/N.

The authors adopt a heuristic approach to portfolio construction. For a given signal each month, they rank order the cross-section of asset classes and calculate the percentile score for each asset class in the opportunity set. Then, for a given threshold θ (set to 50% for the main results), they build an active-weight portfolio relative to the 1/N benchmark by overweighting the asset classes with percentile scores higher than θ, and underweighting those with scores lower than 1–θ. To ensure that the portfolio is balanced, they give equal representation to the respective aggregates of the overweight and underweight investments. Given the no-leverage constraint, they limit the underweight positions for universes with fewer than eight asset classes to 1/2N in order to produce reasonably consistent tracking errors of about 2% a year. Thus, the active weights were held to the range of plus or minus 1/2N, where N, the number of asset classes in the benchmark, is less than eight and plus or minus 1/N where N is equal to or greater than eight.

Because carry and value require longer holding periods to harvest the factors’ returns, the authors take the extra step of setting those strategy portfolios’ monthly weights to the trailing average of the prior-12-months model weights. This step also serves to decrease the required trading and its related costs. In contrast, longer holding periods decay the return potential of a momentum strategy, even after considering turnover. 

To measure risk-adjusted alpha, the authors calculate the residual return based on a six-market-factor model, including four factors from the online Kenneth French Data Library—market beta (RMRF), value (HML), size (SMB), and momentum (MOM)—and two bond factors derived from their data set: the return of long-term Treasuries minus one-month Treasury-bills (TERM), and the return of long-term corporate bonds minus long-term Treasuries (DEF).

Over the 37-year period, most of the strategies earned positive alpha across the three universes. The authors find the most striking results in the diversified universe, in which two of the three individual strategies provided statistically significant alpha at a 5% threshold, and the combined strategy (incorporating all three return drivers) had statistically significant alpha at a 1% threshold. The following exhibit summarizes these main results using data extracted from one of the tables in the article:  

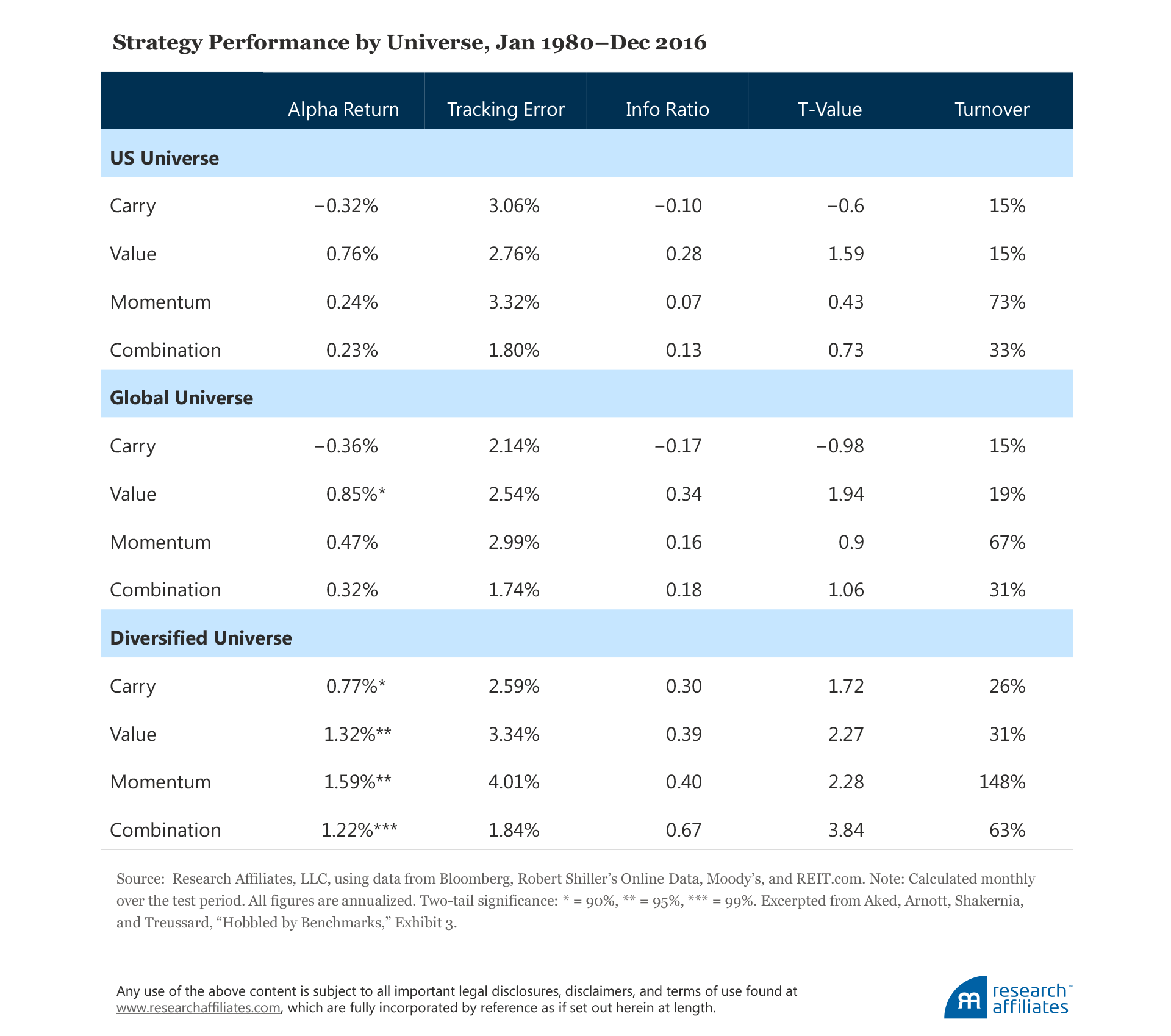
In the article, the authors explain the rationale for their methodological choices, investigate pairs of strategy portfolios, present correlation matrices, and buttress their results with tests of robustness. This synopsis is limited to their major conclusion: a combination of basic factor strategies, constructed to be implementable in an unlevered framework, produced significantly positive returns when applied to a diversified asset-class universe over the 1980–2016 period. This research clearly implies that investors can maximize returns by adopting a TAA strategy in as broad a universe as possible. In light of these results, the fact that investors continue to hobble themselves by adhering to the 60/40 domestic stock/bond portfolio is perplexing. The authors maintain, “A step in the right direction begins with broadening our investment guidelines to permit a benchmark with additional asset classes and to allow symmetric bets both for and against these asset classes.”

Summarized by Philip Lawton, CFA