
Key Points
1. Traditional cap-weighted indices routinely add stocks priced at a high market valuation and sell stocks priced at a deep discount to market valuation—they buy high and sell low!
a. The additions WIN BIG before they’re added; deletions LOSE BIG before they’re dropped. The pattern reverses the year after an index change.
b. As a result, index fund managers can add value either by anticipating changes or by making their trades 3 to 12 months after their peers.
2. Index funds also weight their holdings proportional to price, so their largest holdings usually trade at big premium multiples. As a result, trimming these “top dogs” adds value, too.
3. Stocks are usually added to the index when they’re “hot” and are dropped when they’re deeply out of favor. This sometimes leads to the addition of temporary high-fliers, just before they bomb.
4. We find that two changes in index construction can boost index fund performance:
a. selecting additions based on five-year (or longer) average market capitalization, and
b. using banding to limit flip-flop trades (additions that are quickly deleted), which increase turnover and the related transaction costs that reduce alpha.
Arguments in favor of traditional passive index funds seem compelling. They offer low fees, limitless liquidity, and broad market participation. They match market performance and have negligible trading costs and tracking error—and they beat most active managers, most of the time. ‘Nuff said? Well, no. Apart from the last assertion, none of the descriptions is entirely accurate. Often overlooked in conversations about the travails of most active managers are the avoidable travails indexers face. In this article we will touch on several of the latter, but we will focus particular attention on the fact that index funds buy high and sell low.
Stocks added to capitalization-weighted indices are routinely priced at a substantial premium to market valuation multiples (i.e., buying high), while discretionary deletions (excepting removals related to mergers, acquisitions, and other corporate actions) are routinely of deep-discount value stocks (i.e., selling low). In fact, additions tend to be priced at valuation multiples—using a blend of price-to-earnings (P/E), price-to-cash-flow (P/CF), price-to-book (P/B), price-to-sales (P/S), and (if available) price-to-dividends (P/D) ratios—that average over three times as expensive as those of deletions. This helps explain why from October 1989 through December 2017, the performance of additions lagged discretionary deletions by an average of over 2,200 basis points (bps) in the 12 months following the addition or deletion. Once investors recognize this buy-high/sell-low dynamic, they can avail themselves of some surprisingly simple ways to earn above-market returns.
Zero Trading Costs for the Market Index? Think Twice…
Before we move to our discussion of the buy-high/sell-low dynamic of cap-weighted index funds, let us debunk the notion that index funds have near-zero trading costs (defined as both explicit and implicit costs). To understand this statement, let’s begin with a review of how changes have been made in the S&P 500 Index over its life.
Until October 1, 1989, Standard & Poor’s policy was to announce changes in the S&P 500 after the market had closed, with those changes taking effect at that day’s closing price. No index fund manager could trade before the index had already been altered. As a result, the overnight return variances arising from the different holdings of the index and the index-tracking funds showed up as tracking error for the funds versus the index. Also, any trading costs the index funds incurred in buying or selling the added or deleted stocks showed up as underperformance because they had to trade after the index changes were made at the higher (added stocks) or lower (deleted stocks) prices driven by the resulting shift in demand, reflecting the market impact of rebalancing-related trading. Many empirical studies examined the pre-1989 period and documented stock-price movement immediately after changes were made in the composition of the S&P 500. The first studies revealed and measured the S&P 500 reconstitution effect.1 In the period January 1970–September 1989, on average, additions experienced a positive abnormal return (3.0%) and deletions experienced a negative abnormal return (–1.4%) on the day after the announcement. Index fund trades (and hedge fund front-running of those trades) are the presumptive cause of this 4.4% spread. In October 1989, as illustrated in Figure 1, Standard & Poor’s began pre-announcing changes to the index along with the rebalancing date (known as the “effective date”) when those changes would occur, which could be days or weeks after the announcement date. On the effective date, changes in index holdings are made at the market closing price.
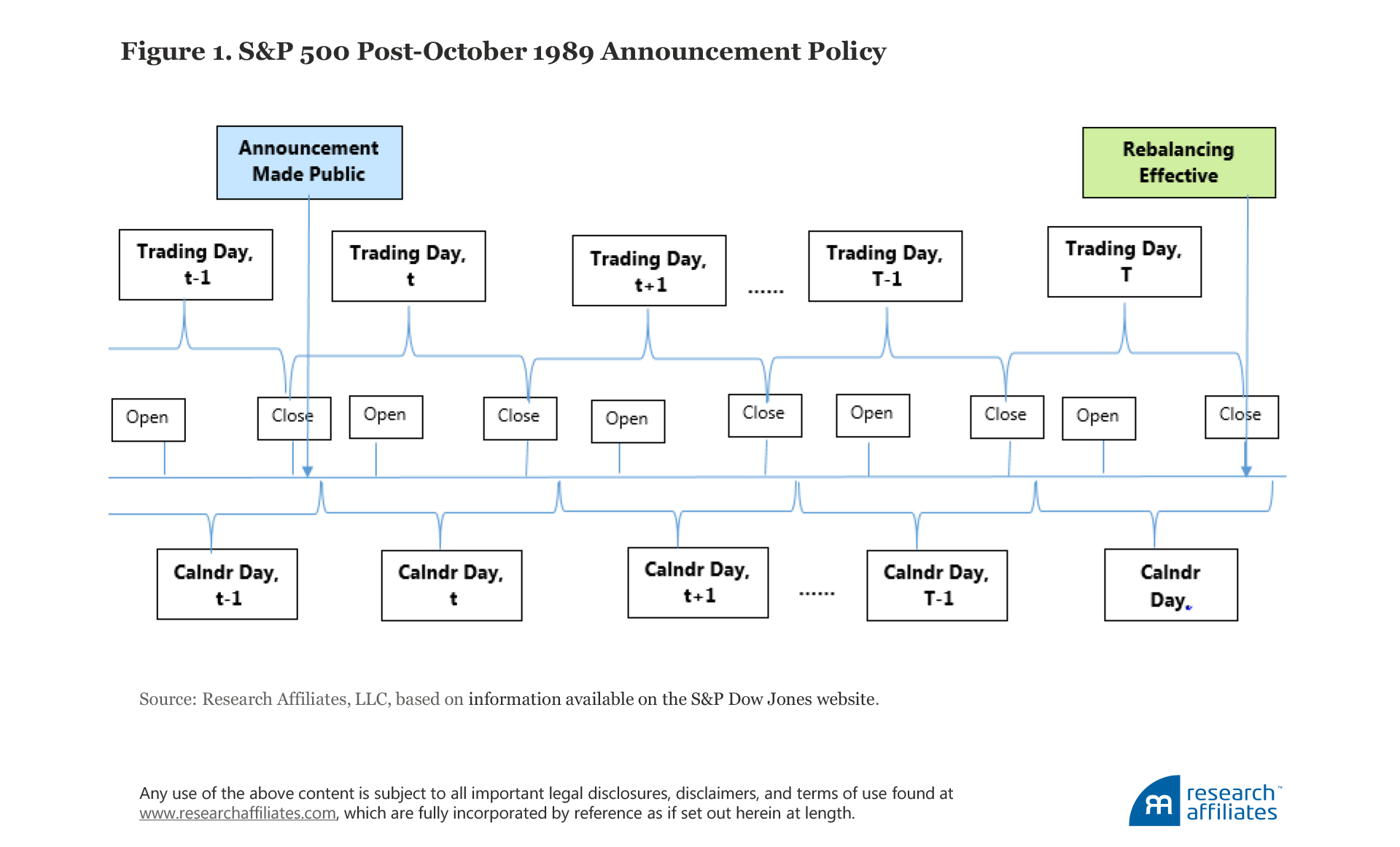
The time between announcement date and effective date provides index fund managers a grace period during which they can make the necessary changes to their portfolios. The grace period gives managers the potential to lower tracking error and to avoid trading costs that otherwise would show up as a performance shortfall. Share prices do move during the grace period—a herd of elephants cannot go through a revolving door without some impact—but the pre-announcement of changes likely has a positive impact on liquidity. Knowledgeable market participants are aware that the large trading size of the stocks bought and sold by index funds on the effective date do not contain any nonpublic information, and thus the price impact from trading should be limited.
Multiple studies (e.g., Lynch and Mendenhall, 1997, and Chen, Noronha, and Singal, 2004) have documented that after index additions are announced, these stocks outperform the market. We find that, for the period from October 1989 through December 2017, additions outperformed the market, on average, by 523 bps over the period between announcement date and effective date. In contrast, we find that discretionary deletions (those not related to corporate actions such as a merger or acquisition) underperformed the market by an average of 429 bps over the grace period. Over one-third of the 952 basis-point spread (523 bps + 429 bps) between additions and discretionary deletions takes place on the last day of the grace period, the effective date itself. From October 1989 through December 2017, the S&P 500 (not the index funds) would have performed 22 bps better a year if additions and deletions were effective immediately at the close preceding the announcement. And were there no grace period, index funds would presumably have underperformed the index by a roughly similar margin.
If we add the day before the announcement and the day after the effective date, both of which exhibit the same pattern of additions outpacing deletions, our 952 basis-point performance spread between additions and deletions soars to 1,315 bps! We find that the performance of additions and discretionary deletions generally reverses, typically starting the second day after the effective date. On average, from October 1989 through December 2017, additions underperformed the market by 128 bps in the 12 months after the effective date, and discretionary deletions outperformed by 2,044 bps. An investor could have adopted the very simple strategy of implementing the additions and deletions to the S&P 500 with a delay of 12 months and in doing so would have outpaced the S&P 500 by 25 bps a year!
Since October 1989, because the S&P 500 is changed after the index funds have presumably completed their trading,2 most index funds benchmarked to the S&P 500 now closely track it. This, unfortunately, is often falsely interpreted as evidence of near-zero trading costs. The dirty little secret is that the transaction costs are still there, and they are huge—they are simply hidden in plain sight.
The trading costs of index funds are masked because they are also borne by the index. During the grace period, the price impact—no matter how large—will affect equally the performance of both the index fund and the index it is measured against. Thus, index funds need not suffer underperformance relative to the index from the price impact of their own trades. The closer a manager trades to the closing price on the effective date, the closer the fund will track the index. Most index fund managers today are far more interested in reducing tracking error than in adding value.
Buy High and Sell Low
Sharpe (1991) pointed out that, in equities at least, active managers’ net-of-cost performance has to equal the market return. It follows from this that, before costs, an active manager can win only if another losing active manager is on the other side of his or her trades.3 Strong evidence exists that losing managers, as a consequence of performance chasing, are legion,4 and finding their shared errors is not difficult. The elephant in the room, often ignored by investors, is the very avoidable buy-high/sell-low dynamic of traditional index fund managers, which causes investors to annually lose, on average, tens of basis points in performance. For investors willing to take a contrarian viewpoint, an alternative path is open within the indexing community. Index investors can capture a modest alpha, readily available, when they choose strategies that mitigate the indexing world’s self-inflicted buy-high/sell-low travails!
Efficient Index for an Efficient Market?
The first index funds appeared in 1973. Early that year, Dean LeBaron of Batterymarch started the first S&P 500 fund for institutional investors, and later in the year, Jack Bogle launched Vanguard Group and created the first S&P 500 fund for retail investors.5 These early index funds were derided by competitors as being “un-American” because they made no effort to discern which firms could make best use of the invested capital or because they believed it was profoundly misguided to deliberately aim for an “average” (benchmark) return.
Time showed, however, that low management fees,6 transparency, and low transaction costs are important features for many investors and, as a result, these features made index funds an extremely popular investing vehicle. By the year 2000, the largest index fund, which was managed by Vanguard, surpassed the largest active fund at the time, the Fidelity Magellan Fund. As of February 2018, the seven largest mutual funds and ETFs by assets under management are allindex funds with the SPDR ETF (“SPY”), which tracks the S&P 500, the largest of them all.
The interest in index funds was initially sparked by the mounting evidence that most active funds underperformed the broad market index, net of fees and trading costs. The move toward indexation was given theoretical support by the efficient market hypothesis (EMH), the belief that stocks follow a random walk and cannot be predicted, and by the capital asset pricing model (CAPM), both of which attained overwhelming popularity in academic circles.7 One of the conclusions of the CAPM is that the market portfolio is mean-variance efficient for a representative investor.8
Shortly after the debut of the first index funds, theoretical arguments and empirical evidence surfaced to demonstrate inefficiencies in the way many index funds were accessing the market. Roll (1977) offered an analysis of the CAPM, subsequently known as “Roll’s Critique,” which challenged the premise of being able to construct a true diversified market portfolio. CAPM asserts that the market portfolio is efficient for a representative investor. But what is the market portfolio?
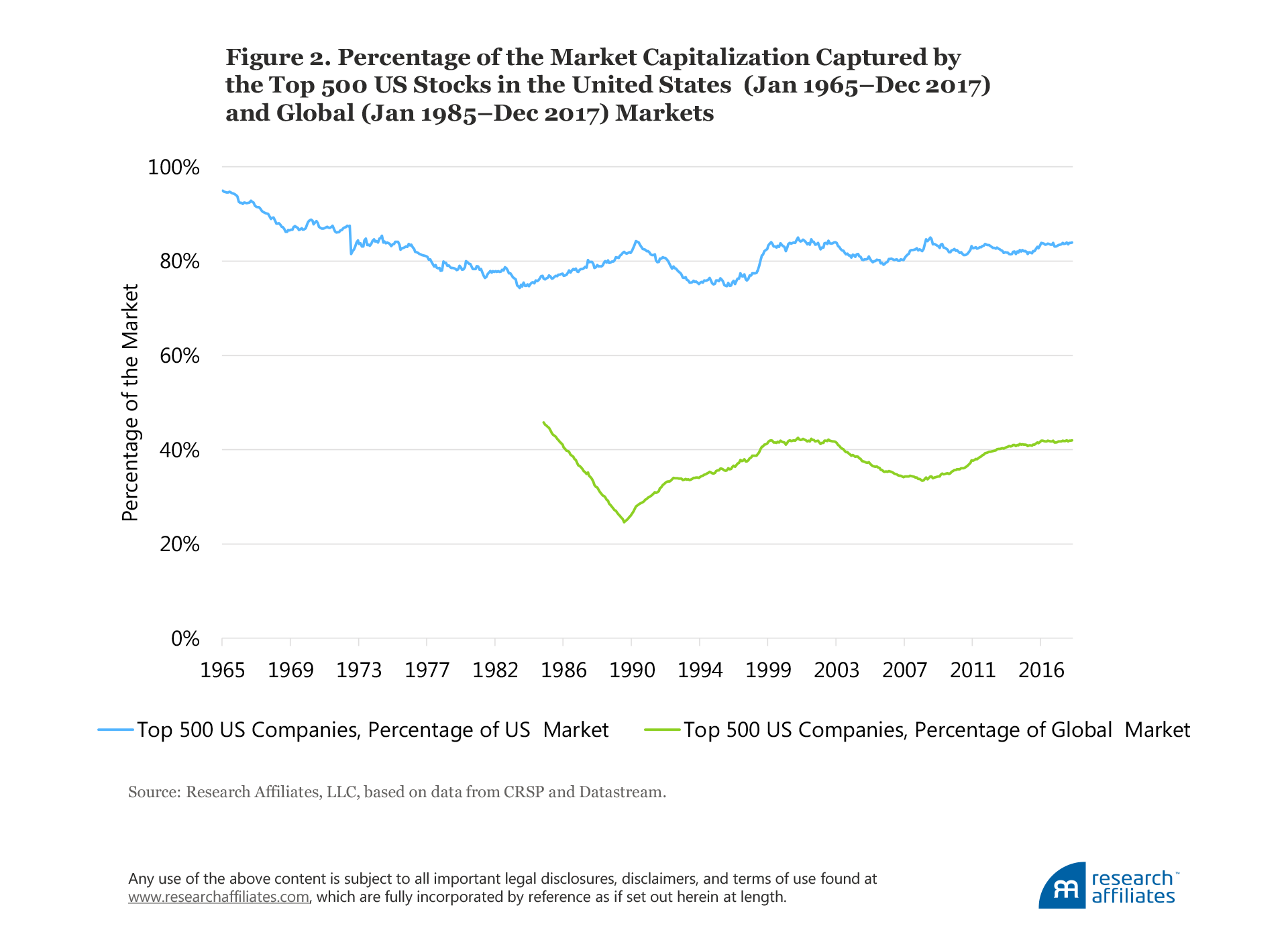
Theoretically, the market portfolio should comprise all the investments we collectively hold as a global community, including our own human capital, real estate, discounted obligations from state-run entitlement programs, and illiquid markets such as venture capital or energy partnerships. Frequently investors in a fund tracking the S&P 500 believe that they are invested in the market portfolio—far from it. Figure 2 shows the market size of the 500 largest US companies as the fraction of the US market from 1965 through 2017 and as the fraction of the global equity market from 1985 through 2017. On average, these companies only capture about 80% of the US equity market and about 40% of the global equity market, respectively, let alone the total of the investable market.
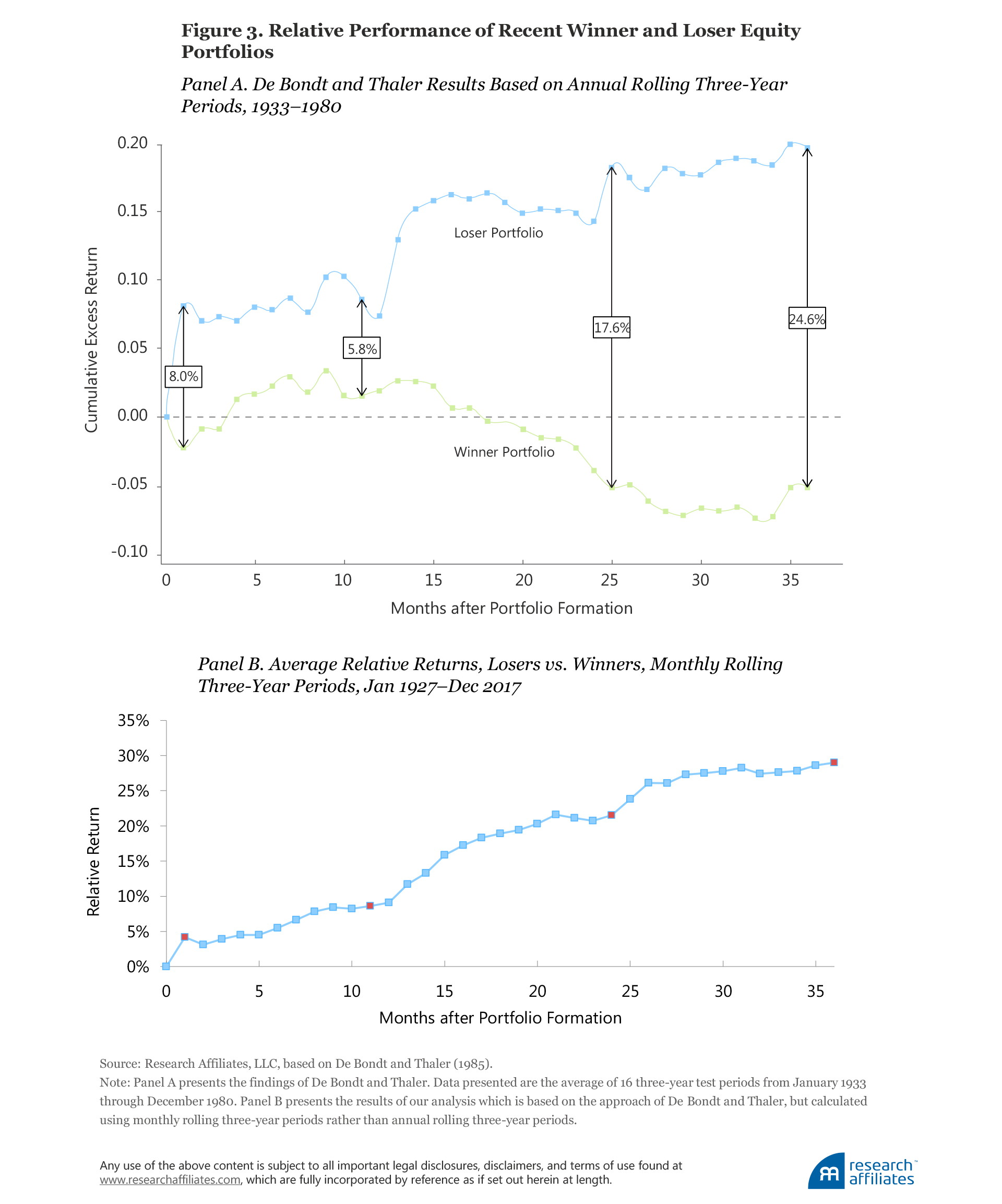
At the time the first index fund was created, the best empirical evidence was that stock prices largely followed a random walk and thus the return of any stock is unpredictable. But by the early 1980s, evidence of stock return predictability began to surface. De Bondt and Thaler (1985) showed that stock returns exhibit a strong pattern of reversion to the mean. They constructed a portfolio of the most recent “winner” stocks and a portfolio of the most recent “loser” stocks. De Bondt and Thaler’s original results are presented in Figure 3, Panel A. Over the long run, the recent winner portfolio underperforms, while the recent loser portfolio outperforms.9
We reproduced the cumulative excess returns relative to the S&P 500 for the two portfolios in De Bondt and Thaler’s original study. Following De Bondt and Thaler, we did not adjust for trading costs. Although trading costs may be material, they will be far smaller than the 2,400 basis-point return spread between the two portfolios by year 1980. This should not be at all surprising except to efficient-market true believers, because any recent winner stocks tend to be relatively expensive and any recent losers tend to be relatively cheap.
De Bondt and Thaler relied on an average return across annually rolling three-year periods (i.e., January 1933 through December 1935, January 1934 through December 1936, and so forth). Therefore, any calendar effects—notably, the January effect—should show up in their results, as illustrated by the jumps in months 1, 13, and 25. Our replication of their work uses monthly rolling three-year periods (i.e., January 1933 through December 1935, February 1933 through January 1936, and so forth) and spans over 90 years of data, including the first three-year “seed” span from January 1927 through December 1929, and the last three-year result span from January 2015 through December 2017. Our results, presented in Figure 3, Panel B, vividly reinforce the findings of De Bondt and Thaler with far higher statistical significance because the seasonality disappears, and should dispel any illusions that the market is efficient, at least with regard to the tendency for mean reversion in long-term price movement.
Top Dogs Disappoint
The results of our analysis have implications for index fund rebalancing in which cap-weighted index funds buy recent winners and sell recent losers. This dynamic hurts index fund performance, as we shall demonstrate shortly.10 In a similar fashion, cap-weighted index funds also “own high and shun low,” aptly illustrated by their holding the largest market-cap stocks in the world, which also carry the largest weights in a cap-weighted portfolio.
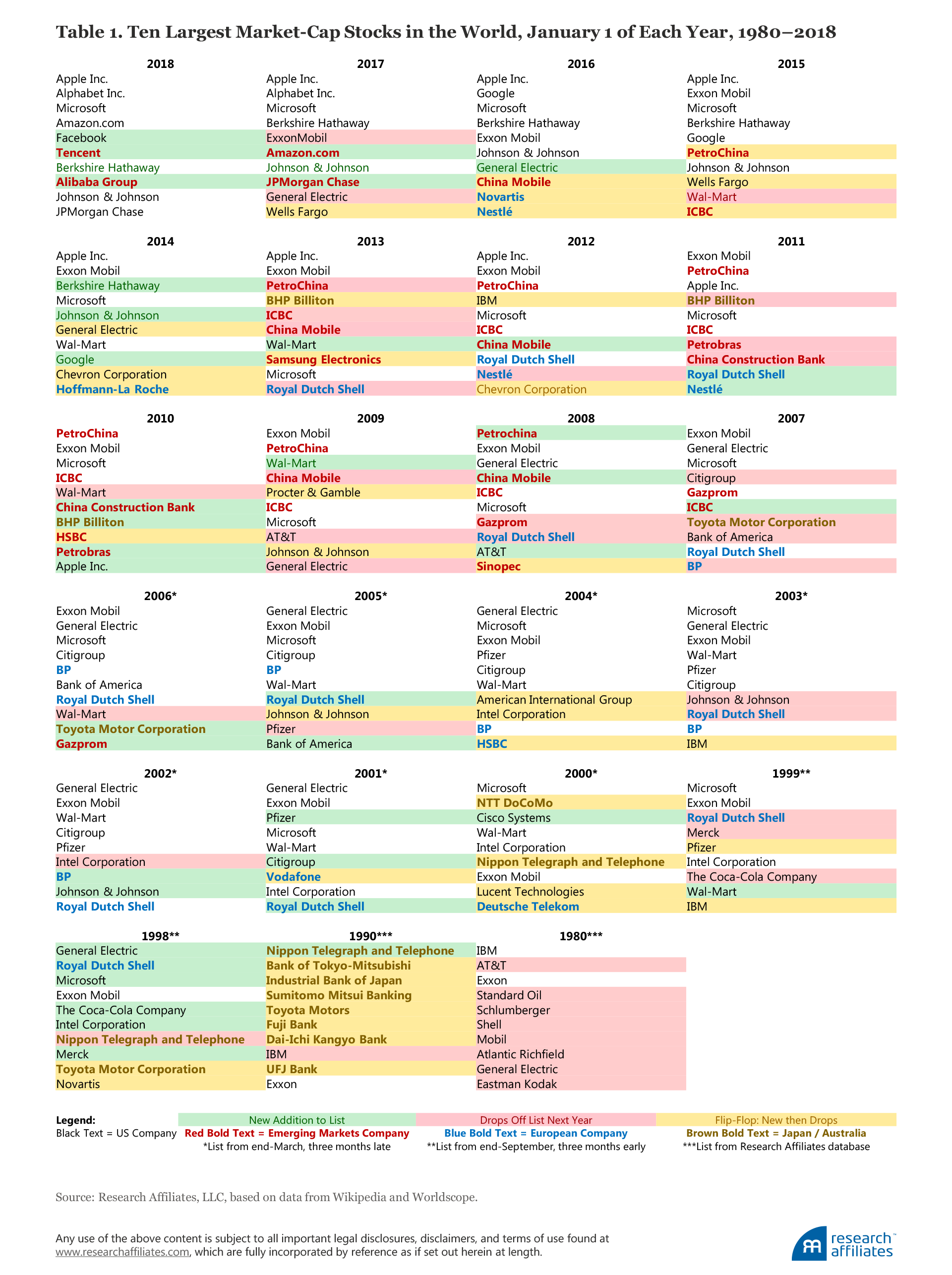
Let’s look back year by year over the last 20 years, and include 1990 and 1980 for good measure. Table 1 shows that the rotation of the top 10 largest market-cap stocks in the world has been prodigious. Of the 10 largest in 1980, just 2 stocks (IBM and Exxon) were still on the list in 1990. Of the 10 largest in 1990, just 2 (Japan’s National Telephone and Telegraph, or NTT, and Exxon) were still on the list in 2000. Of the 10 largest in 2000, just 2 (Microsoft and Exxon-Mobil) were still on the list in 2010. Of the 10 largest in 2010, just 2 (Microsoft and Apple) were still on the list at the start of 2018. Finally, in the most recent and extreme 10-year span, only 1 of the top 10 market-cap stocks in 2008 (Microsoft) remained on the list at the beginning of 2018.
On average, only 3 stocks in the top 10 list when ranked by global market cap remain on the list 10 years later. The 7 companies that fall off the list reliably underperform the 7 newcomers that take their place, and importantly the 7 dropouts have a larger weight at the start of the 10-year period than the 7 additions that replace them. Almost all of the 7 deletions also underperform the MSCI All Country World Index (ACWI) in the year they fall off,11 and the great majority are serious performance laggards over the decade in which they are replaced.
The top company, the first on the list, almost always remains somewhere on the list 10 years later—but never in the pole position—and almost never outpaces the ACWI over the same 10 years. The other 2 survivors may be lower or higher on the list, and may be either an outperformer or an underperformer. If the number one stock, and the 7 dropouts, all reliably underperform, that leaves 2 stocks with 50/50 odds. It follows that roughly 9 of the top 10 largest holdings in a global cap-weighted portfolio will underperform on a 10-year basis. Betting against these 10 top market-cap stocks in the world can be a useful strategy.
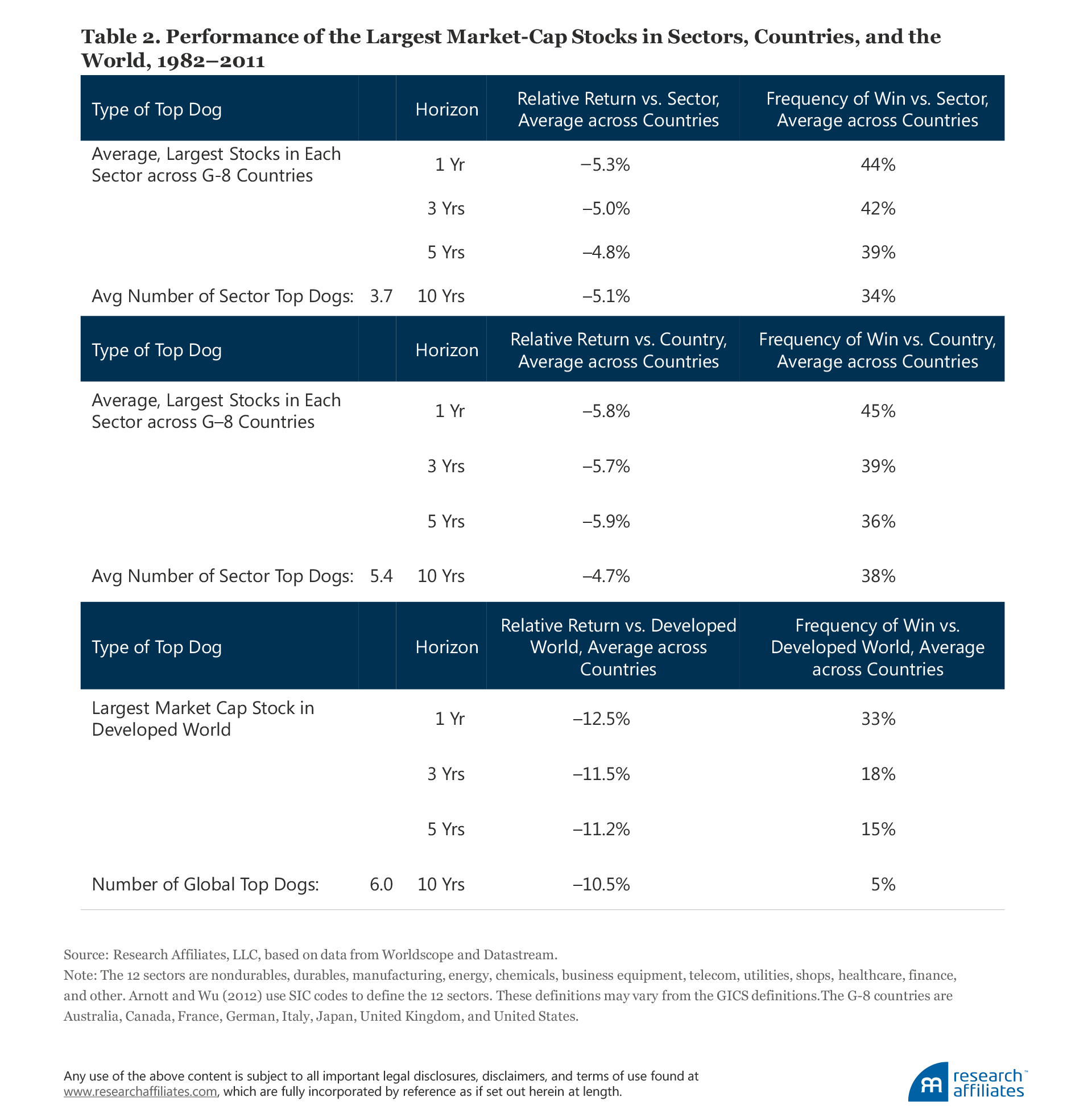
Arnott and Wu (2012) studied the performance from 1982 to 2011 of the largest market-cap stock (the “top dog”) in each of 12 sectors, in each of the G-8 stock markets.12 Although our sample period comprised only three non-overlapping 10-year spans, we had nearly 300 relatively independent samples (three unique 10-year periods, eight countries, and 12 sectors). Accordingly, these results have high statistical significance.
The sector top dogs compose an average of 34% of their respective sector, and on a 10-year basis underperform their equal-weighted sectors by an average of 5.1% a year across 12 sectors and eight countries as shown in Table 2. Over a decade, the underperformance compounds to just over a 40% loss relative to these companies’ sector returns. The largest-cap stock in each country has near-identical performance to the sector top dog, lagging their home stock market by 4.7% a year, with only 38% outperforming their home market.
The global top dog, the stock with the largest market cap in the world, exhibits the most extreme outcome. History suggests that the number one stock is almost always 1) a big company, 2) trading at an elevated multiple, and 3) subject to adverse shocks as competitors and regulators seek out its Achilles’ heel. The global top dog outpaced the global cap-weighted stock market only 5% of the time over the 30 years of the study, and delivered an annual shortfall of 10.5% a year—equivalent to losing two-thirds of its value relative to the overall market in just 10 years. Even with only three non-overlapping spans, six different global top dogs emerged. This result falls short of statistical significance, but only the most fervent disciple of efficient markets would not find this outcome disturbing.
Would most rational investors want to own a portfolio in which the largest holding has a 95% likelihood of underperforming over the next 10 years? Or in which the largest holding in each sector or each country is likely to underperform by 5% a year over the next decade? Or a portfolio in which each of the top 10 stocks has roughly 90% odds of underperforming the rest of the portfolio? No.
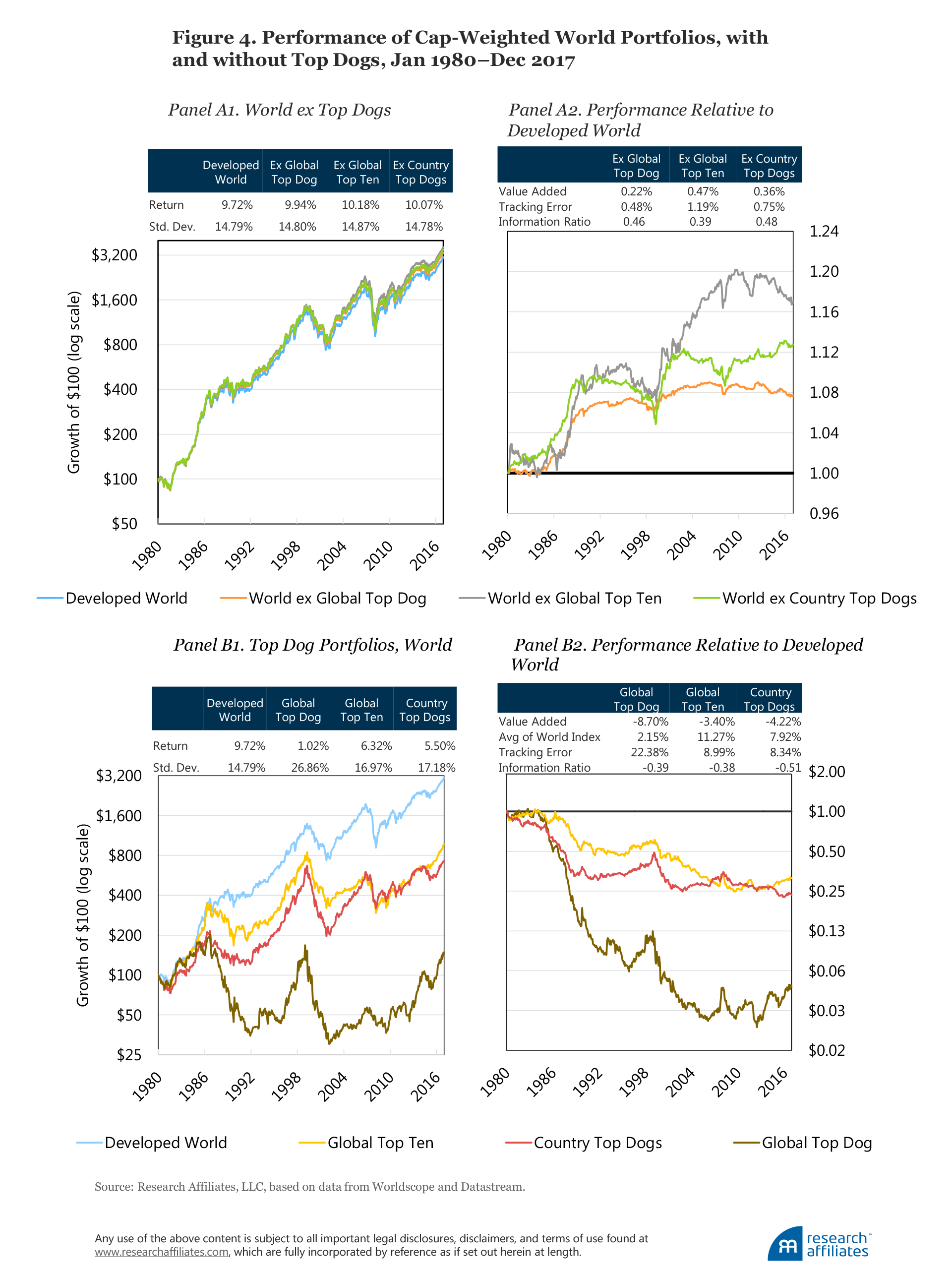
We examine the performance of four portfolios from January 1980 to December 2017 and compare the results in Figure 4:
- Developed World Portfolio, Cap Weighted (“World”)
- World, excluding the single largest market-cap stock in the world
- World, excluding the 10 largest market-cap stocks in the world
- World, excluding the largest market-cap stock in each country
We find that excluding each of the three top-dog categories improves performance relative to the World portfolio, but also increases the tracking error, which means that the reliability of the strategy wanes as each market-cap category is excluded. Over the last half-decade holding the largest market-cap stocks has not hurt performance. Have markets suddenly caught EMH religion? Or have growth stocks been on a roll globally, beating value stocks by some 2.5% a year for the last 11 years (using MSCI World Growth versus Value)? We would argue that if this is the best mega-cap stocks can do with a powerful tailwind from growth beating value, the recent benign results for mega-cap names is hardly a basis for complacency.
Estimating the Cost of Buy-High/Sell-Low Indexing
Just how much are investors losing because of mean reversion in stock prices and transaction costs? The S&P 500 is the natural starting point for our analysis because of its stature as the basis for the first index funds and is today the most tracked index by total assets.
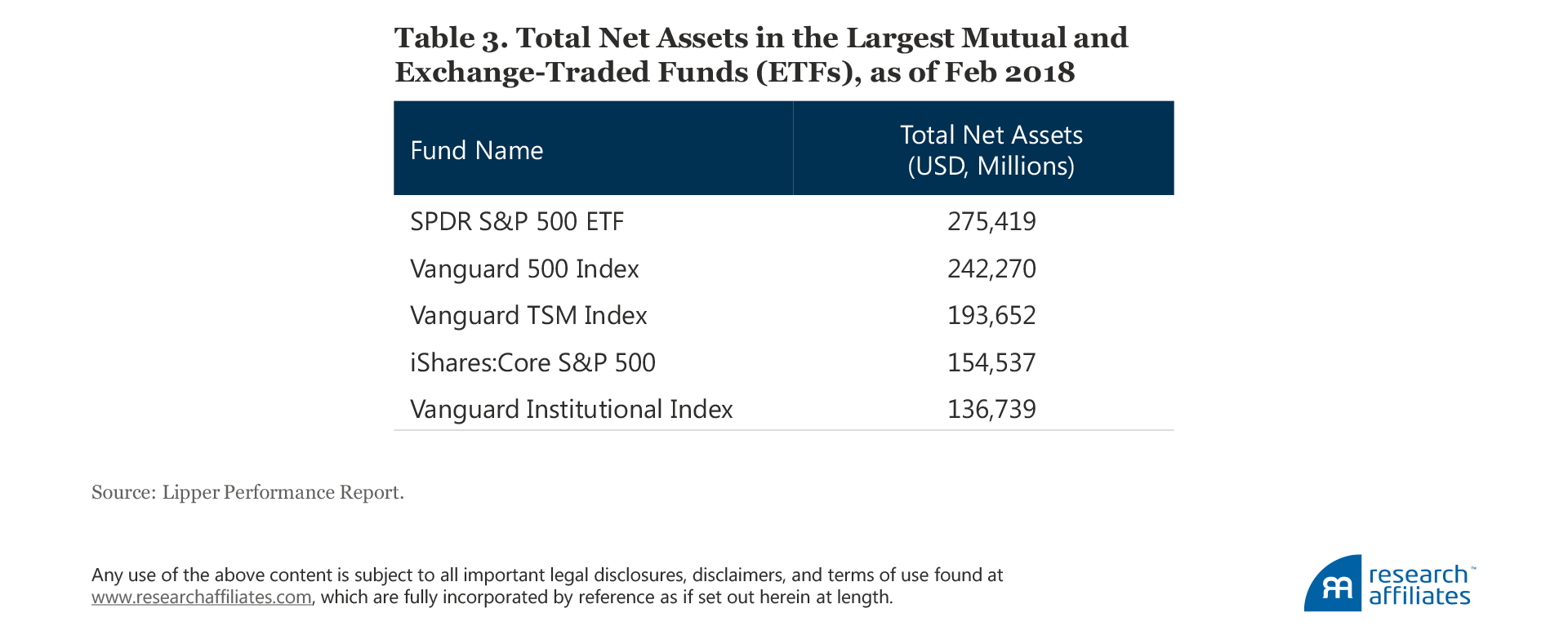
Broad market indices were not originally created to be investment strategies. They were created to measure the performance of the stock market. When Standard & Poor’s launched the S&P 500 in 1957, their management team hardly expected trillions of dollars would be invested in strategies that track it.13 Yet according to our estimates, by the end of 2017, $4.1 trillion was indexed to the S&P 500 alone.14 In Table 3, we list the top five US mutual funds and ETFs, which are all cap-weighted index funds, and their total net assets as of February 2018.
The average historical one-way turnover of the S&P 500 is 4.4%. Turnover of 4.4% on $4.1 trillion of assets implies that on the days the index rebalances, roughly $360 billion in stock trades, on the bid and ask sides combined, takes place, with all trades concentrated in a short list of additions and deletions.15 Also, about $6.5 trillion in additional assets are likely being benchmarked to other cap-weighted indices, and many of the benchmark-hugging active managers—as well as hedge funds front-running the index fund trades—may also jump on the same trades as the index funds.16
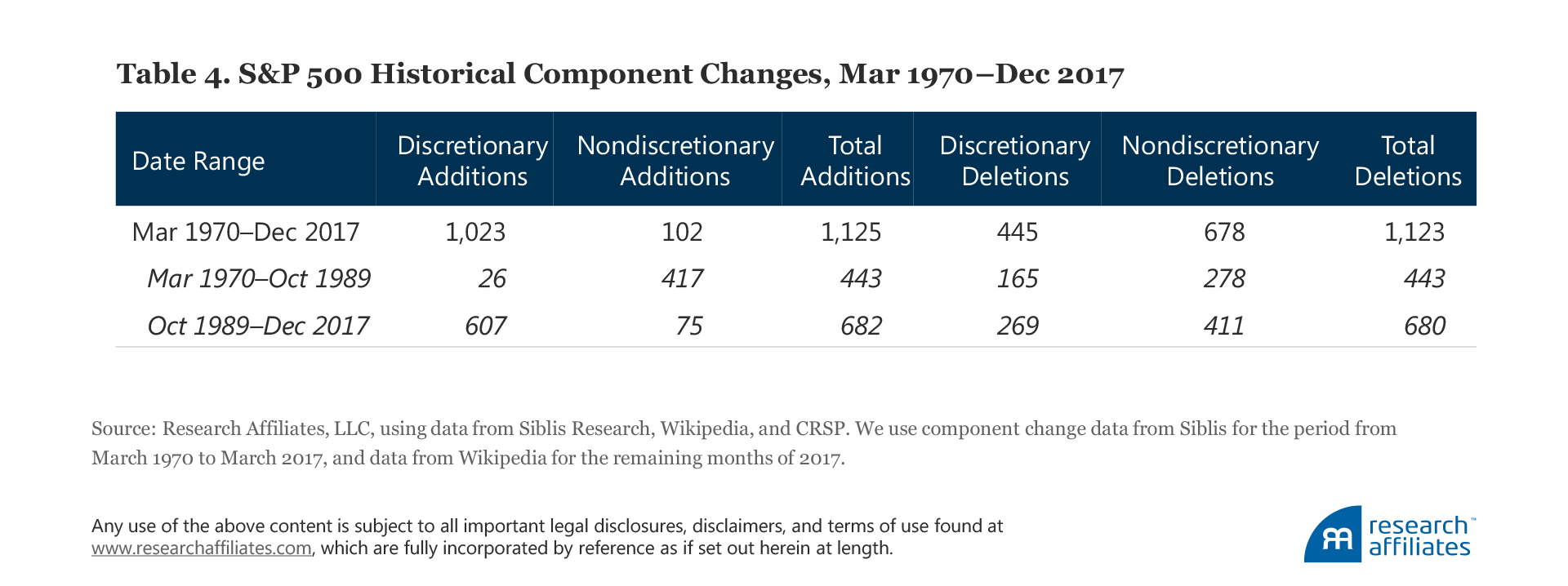
As a first step in estimating the true cost of indexing, we constructed a sample of the S&P 500’s historical component changes based on data from Siblis Research and Wikipedia.17 The sample of historical component changes consists of 1,125 additions and 1,123 deletions from March 1970 to December 2017.18 We use stock return data as a proxy to determine the nature of the changes: nondiscretionary changes due to merger, spin-offs, or acquisitions, and discretionary changes made by the S&P Index Committee following the S&P 500 guidelines.19
In our analysis we focus on the period before and after October 1989, when Standard & Poor’s changed the rebalancing procedure by introducing a grace period between announcement of index constituent changes and their effective date. Over the full sample, the vast majority of additions are discretionary with just 102 being nondiscretionary (e.g., company spinoffs, such as the AT&T breakup in the 1980s), compared to over half of the deletions being nondiscretionary (e.g., bankruptcies and mergers), at 678, and 445 being discretionary.
The much larger number of nondiscretionary deletions compared to nondiscretionary additions is a reflection of corporate actions: large companies are more likely to consolidate their businesses or to be acquired (the main sources of nondiscretionary deletions) compared to spinning off a large segment of their business (the main source of the nondiscretionary additions). We provide more detail on the nature of additions and deletions by subperiod in Table 4.
A company’s inclusion in the S&P 500 is determined by the S&P Index Committee following guidelines for stock selection on size, liquidity, minimum float, profitability, and balance with respect to the market (Blitzer, 2014). Because the objective of the index is to track 500 of the largest companies by market capitalization, we should expect the stocks of companies entering the portfolio to have had an increase in price and thus the company to have had a coincident rise in market capitalization. Conversely, a deleted company’s stock has typically experienced a price decline, and hence, the company has experienced a reduction in market capitalization.
In our analysis we measure stock performance. When we examine pre-announcement performance, as reported in Table 5, Panel A, we observe that additions, on average, outperform deletions monotonically with the gap between additions and deletions accumulating to 63.80% over the 12 months prior to the announcement. This is not a typo. New additions beat the market by 36.17% and discretionary deletions underperformed by 27.63%. This magnitude of over- and underperformance gets the attention of the S&P Index Committee.
Following the pre-announcement of changes to the index over the period exclusiveof the rebalancing date, as shown in Table 5, Panel B, additions, on average, appreciate by about 3.94% relative to the market, while deletions trail the market by 1.75%, producing a performance gap of 5.68%. This pre-announcement, or grace period, return is partly driven by index fund managers who are willing to accept some tracking error to begin early purchasing of the new and old stocks, and partly by liquidity providers accumulating shares to supply them at a later date to the index funds. This dynamic has driven a common hedge fund strategy. Of course, part of the price moves may be due to other sources, such as improved analyst coverage or an increase in future liquidity.
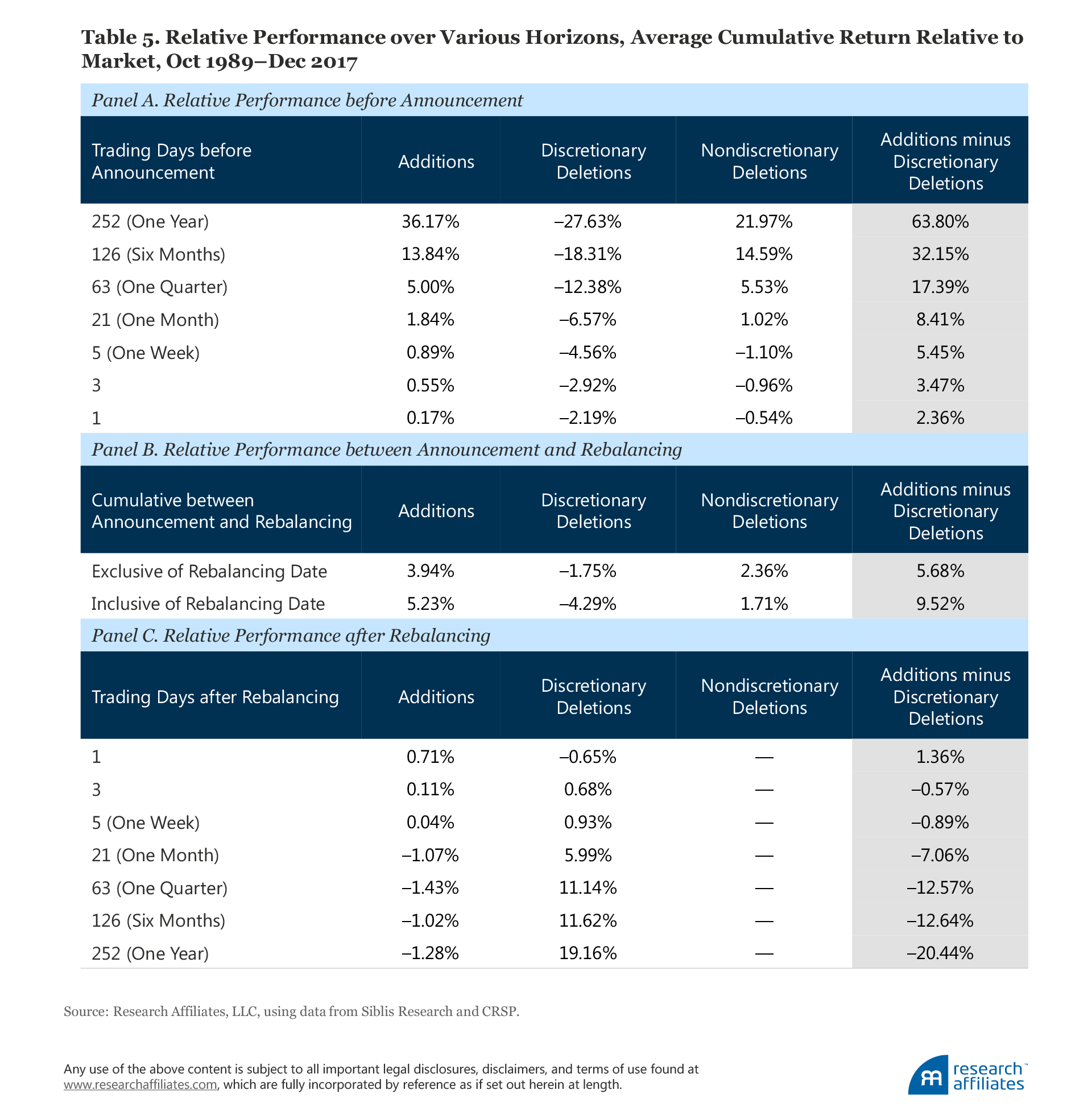
Following the pre-announcement of changes to the index over the period inclusiveof the rebalancing date, also reported in Table 5, Panel B, the additions beat the market by an additional 1.29% while the deletions lagged by an additional 2.54%. From the announcement date to the market close of the effective date, the performance of additions is ahead of the performance of discretionary deletions by 9.52%. Whereas for additions most of the change in price happens before the effective date, for deletions most of the price movement takes place on the effective date. We surmise that the cost of shorting perhaps dissuades many liquidity providers from pre-trading index deletions.
Notably, this price movement immediately precedes the announcement date and continues in the first day after the effective date. While we might surmise that the selection of discretionary additions and deletions is partly motivated by the performance spread between the additions (past winners) and deletions (past losers), this hypothesis would not explain the impressive performance gap in the week—and even in the day—before the announcement is made. The one-year performance gap is about 25 bps a day, and the six-month and three-month gaps are of similar magnitude. The gap widens, however, to 236 bps on the single day before the announcement, and to over 5% in the week before the announcement.
Cynics might wonder if word is leaking out about a pending change in the index. We believe a more plausible explanation is that hedge funds (and some index fund managers) make educated guesses as to likely index changes. On the day after the effective date, we find another 1.36% performance spread in favor of the additions, perhaps due to catch-up trades by index funds that did not complete their additions and deletions on the effective date. If we add the performance spreads on the day before the announcement and the day after the effective date, the 9.52% performance spread between additions and deletions soars to over 1,300 bps! Indexing has much merit and many advantages, but those who claim that changes in the index do not move share prices have some explaining to do.
In the first year (or in the 252 equity market trading days) following the effective date, additions suffered a modest performance drag of 1.28%, while the deletions outperformed the market by 19.16%, a performance difference of 20.44% (Table 5, Panel C). If we exclude the first day after the effective date, when the additions continued to outpace the deletions, discretionary deletions beat additions by 21.80%.
We find the post-rebalancing reversal of performance for the additions and deletions unsurprising when we examine the valuation ratios of additions and deletions relative to the market, as shown in Table 6.20 The additions, based on an average of P/B, P/E, P/CF, P/S, and P/D, are 74% more expensive than the market. The discretionary deletions, in contrast, are 50% cheaper than the market based on the combination of the five valuation measures. When the additions are 3½ times as expensive as the discretionary deletions, the performance spread of over 20% between the additions and discretionary deletions in the subsequent year is nothing more than a combination of the value effect and mean reversion.
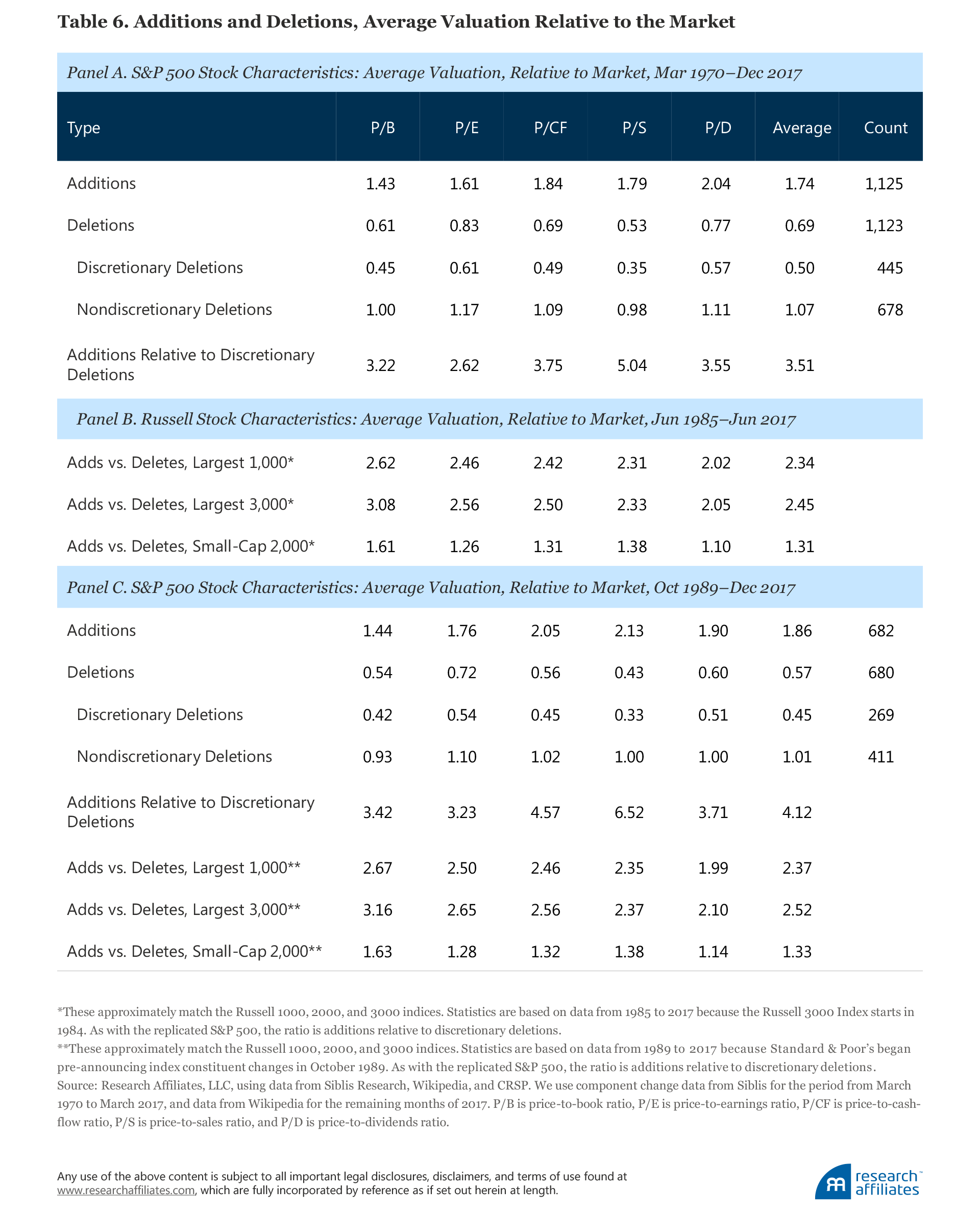
We also show summary statistics for replications of the Russell 1000, 2000, and 3000 indices. These are not as precise as our replication of the S&P 500, which we will describe shortly. For the cap-weighted 1000, 2000, and 3000 indices, we rebalance each year at the end of June, and we use market capitalization, not float; the results for the actual Russell indices should be very similar. As we might expect for a broad index (the Russell 1000 and Russell 3000), the effect is milder than for the S&P 500, but is still shockingly strong.
Why is the effect so much weaker for the Russell 2000? Consider that additions to the Russell 2000 can be promotions from the micro-cap list (previously not even qualifying for the Russell 3000) or they can be demotions from the large-cap Russell 1000. The former will usually be priced at lofty multiples, while the latter will have fallen into the Russell 2000 because of depressed valuation levels. Likewise, deletions, if they’re not forced deletions as a consequence of corporate actions, will be either promotions to the Russell 1000 (typically expensive) or demotions out of the Russell 3000 (typically cheap). Promotions to and demotions from the Russell 1000 will be a minority of the trades, but these trades (buy low, sell high) will be large, and promotions from and demotions to the micro-cap list (buy high, sell low) will be more numerous, but small. Consequently, the buy-high/sell-low phenomenon is largely canceled.
The buy-high/sell-low pattern of the S&P 500 is demonstrated for the period October 1989–December 2017 in Figure 5, Panel A, which graphically replicates the results in Table 5. The stocks added to the index beat the market, on average, by 30% in the year prior to the rebalancing date, while the stocks sold by the index lagged the market by about 45% over the same period. After the rebalancing date, this situation reverses, and the deletions beat the additions by over 20%, with the lion’s share of the difference coming from the deletions.21
Figure 5, Panel B, illustrates the return pattern over the period from March 1970 through September 1989 when changes to the index were implemented after the close of the announcement. We mark the period between the announcement close and the rebalance close in grey to indicate that in the pre-1989 period no gap existed between these two events. As Panel B illustrates, in the earlier period the stocks that entered and left the index did not exhibit as pronounced a return pattern: additions did go up in price, but by a lesser magnitude, and the prices of deletions remained flat. We speculate that before October 1989 the S&P Index Committee recognized the buy-high/sell-low rebalancing dynamic of changes in their cap-weighted index and perhaps sought to minimize the performance impact.
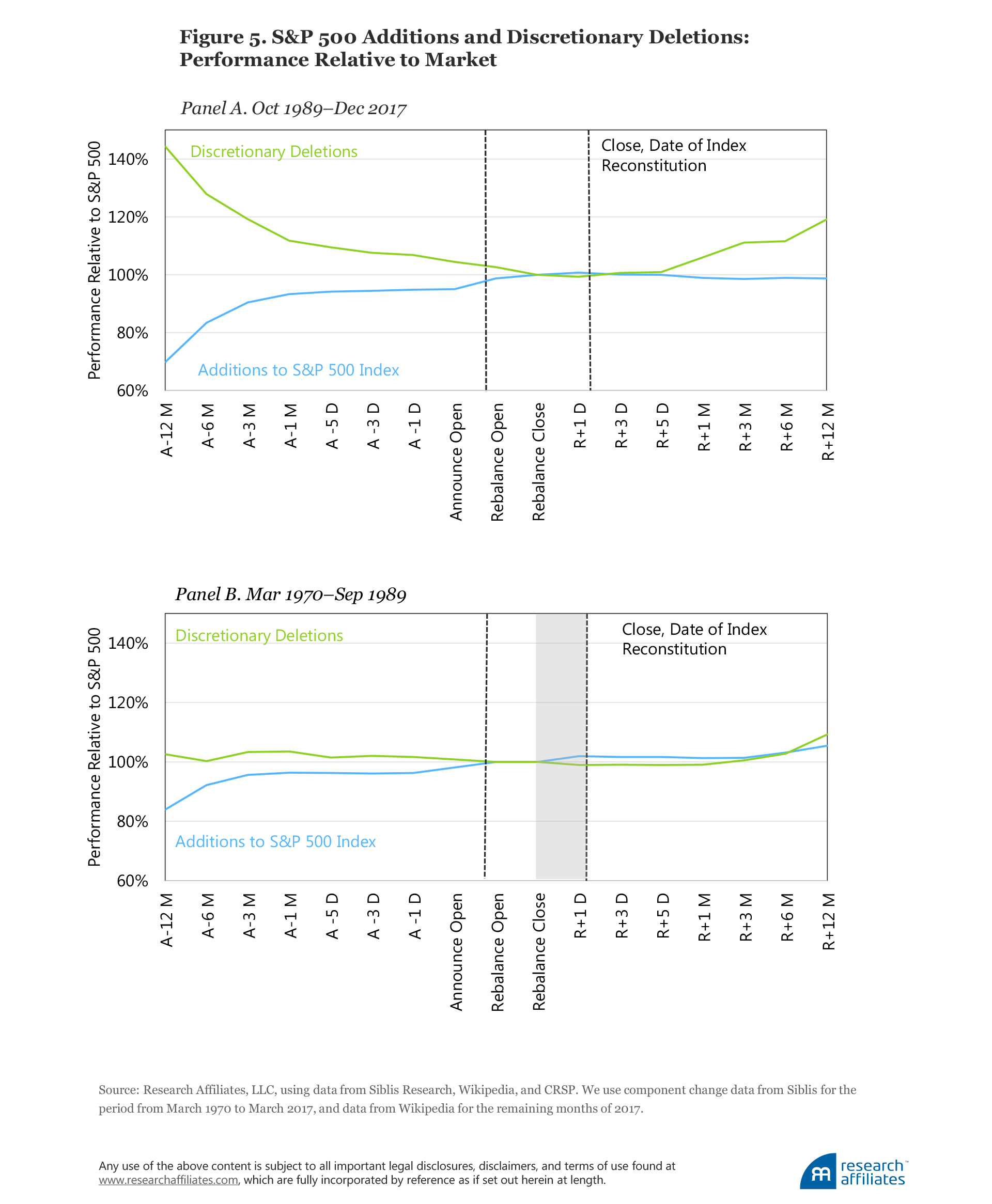
The charts in Figure 5 show that prior to October 1989 the difference in returns between the additions and deletions was small before a change was announced, and negligible afterward, but after October 1989 both effects became far more pronounced. Was the post-1989 policy change driven by client pressure to see more glamour stocks in the index funds? We doubt we will ever learn the true reason for the change.22
A More Efficient Market Index
Using the S&P 500, we have shown that the buy-high/sell-low dynamic of traditional large-cap indices can hurt investors 1) because of the price impact from billions of dollars of stocks being traded on index rebalancing dates, and 2) from mean reversion in stock prices. Broader indices such as the Russell 1000 and Russell 3000 exhibit the same effect, albeit modestly weaker. How large are the impacts of these two forces on index return and investor wealth? To answer this question we simulated three indices based on the actual S&P 500 and progressively introduced changes to each of the simulated indices to gauge the effect of each change.
The three simulated indices are 1) a replication of the S&P 500; 2) a replication that adjusts the first replicated index so that trades occur on announcement date rather than on effective date; and 3) a replication that delays trades by a 3- or a 12-month lag (which we call “lazy”) after a large portion of the mean reversion in price has taken place.
Actual S&P 500. Stocks in the index are weighted based on their market capitalization, adjusted for float to reflect the portion of the market capitalization available to the general public. This float adjustment was introduced in March 2005 and fully transitioned in September 2005, prompted by the growing number of new tech companies, which are closely held by their founders. Before this change the index weights were based on simple market capitalization, adjusted from time to time to allow for stock buybacks and secondary equity offerings.
Replicated S&P 500. We do not have precise daily data on the S&P 500 constituents and weights. We do have data on the component changes (i.e., the additions and deletions to the index), which we have collected from open sources such as Siblis Research (until March 2017) and Wikipedia (for the period April–December 2017). We begin our replication of the S&P 500 with a yearend 2017 snapshot of SPY ETF holdings. Then, using the history of component changes as a guide, we roll backward in time over the past 28 years to October 1989, periodically cross-checking the simulated holdings against the holdings of the SPY ETF (or the Vanguard 500, when SPY ETF holdings are not available to us). In our replication periods, as we roll back before September 2005, we shift from a weight based on the current-float-adjusted S&P 500 to a weight based on market capitalization.23
Of course, despite our efforts to match the original index, this replication procedure will still be imperfect. The most noteworthy sources of differences are 1) the lack of the exact index holdings and exact stock weights; 2) our rolling back from current float-adjusted weights, which do not track perfectly with the changes in the float between 2005 and yearend 2017; and 3) our use of market capitalization, unadjusted for the float information, when float information is unavailable, as we move from 2017 to 2005. That said, the replicated S&P 500 matches the actual S&P 500 with an R2 of 0.9997. The annualized performance since October 1989 differs from the published S&P 500 performance by a scant three basis points a year, and average annualized volatility is also within three basis points. It’s a pretty good match!
Replicated Trade-on-Announcement S&P 500. Before October 1989 the changes to the index were executed at the close of the announcement day. We wanted to know how the S&P 500 would have performed if it still followed this protocol. To gauge the performance impact of the grace period, we computed the replicated trade-on-announcement S&P 500 by modifying the replicated S&P 500 to have trading occur at the close of the announcement date instead of at the close of the effective date. Practically, no index fund could do this, but an index calculator certainly can, exactly as they did before October 1989. Of course, unless an investor has the private information from Standard & Poor’s on the exact announcements of additions and deletions, and their timing, this strategy cannot be replicated. Nevertheless, the exercise is still valuable for analytical purposes. The difference in performance between this index and the replicated S&P 500 is probably a useful, if crude, approximation of the trading costs actually experienced by index fund investors.
Lazy Replicated S&P 500. The actual S&P 500 buys stocks at lofty valuations and sells them at deeply depressed valuations. The index performance suffers as the prices subsequently revert to the mean. We simulated a lazy replicated S&P 500 that delays trades by several months (we show results for 3 and 12 months) after a large portion of the mean reversion in price has occurred. Delaying trading inevitably causes tracking error versus the actual S&P 500. Unlike the trade-on-announcement index, the lazy index is easy to implement and the difference in its performance versus the replicated S&P 500 captures the impact of mean reversion on index performance.24
Why Lazy Is Good for Index Fund Management!
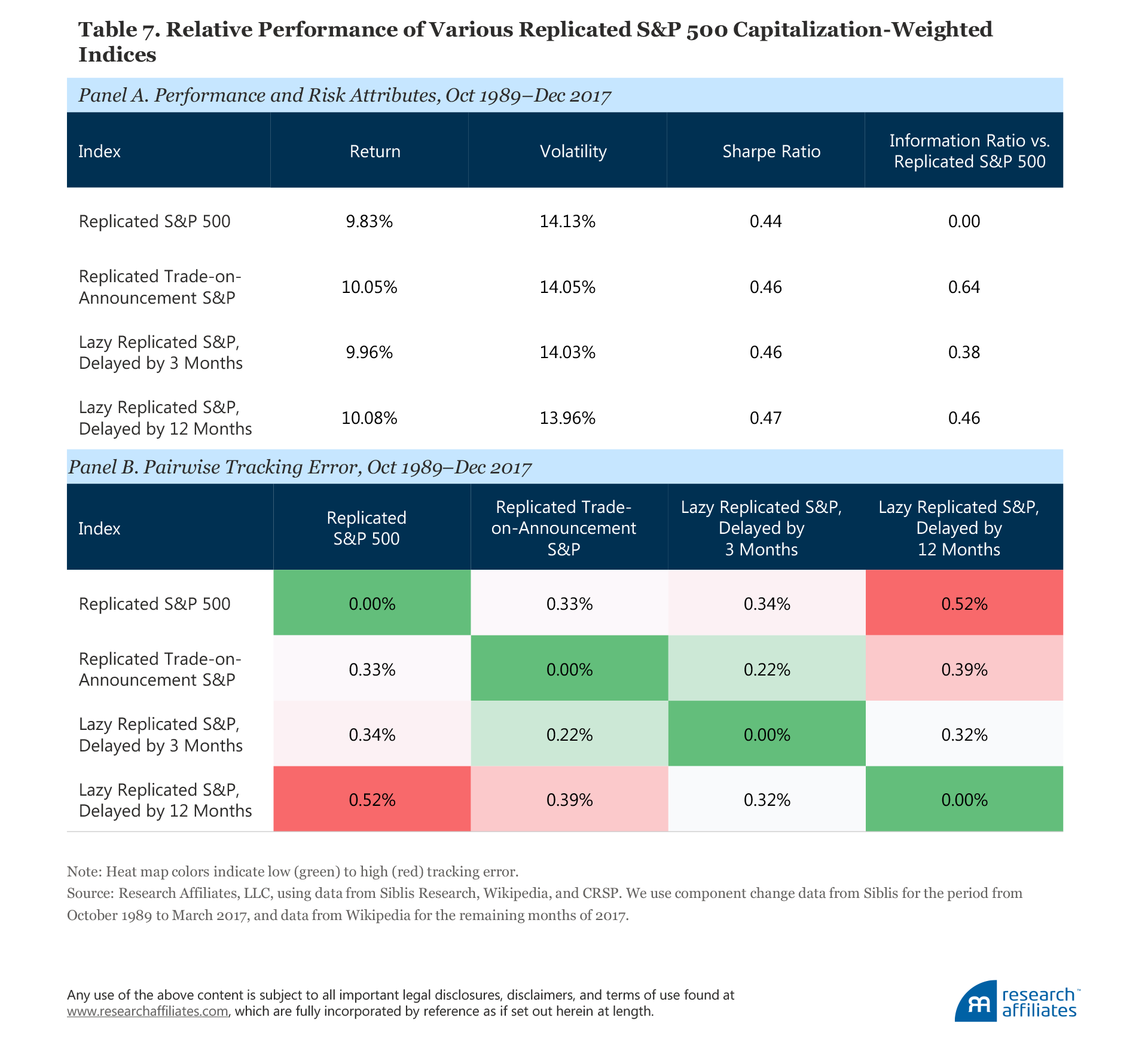
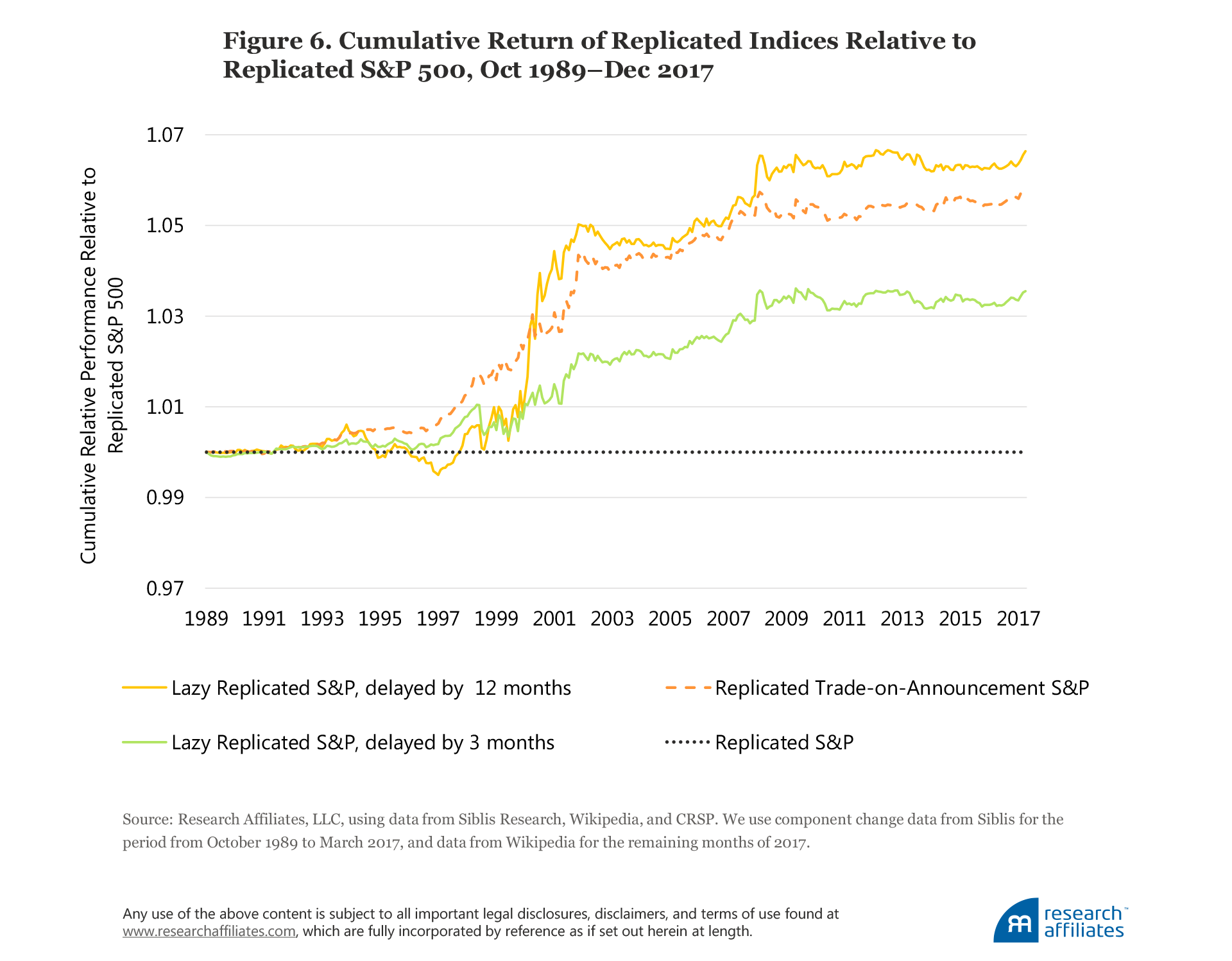
We display the performance characteristics of the replicated S&P 500 indices from October 1989 through December 2017 in Table 7 as well as their dollar-growth paths relative to our replicated S&P 500 in Figure 6. Figure 6 graphically illustrates the efficacy of the simple approaches we explore to improve index fund results, the consistency of results, and the times when lazy strategies fail (notably, during growth-dominated bubbles).
Using the S&P 500, we have shown that the buy-high/sell-low dynamic of traditional large-cap indices can hurt investors 1) because of the price impact from billions of dollars of stocks being traded on index rebalancing dates, and 2) from mean reversion in stock prices. Broader indices such as the Russell 1000 and Russell 3000 exhibit the same effect, albeit modestly weaker. How large are the impacts of these two forces on index return and investor wealth? To answer this question we simulated three indices based on the actual S&P 500 and progressively introduced changes to each of the simulated indices to gauge the effect of each change.
The three simulated indices are 1) a replication of the S&P 500; 2) a replication that adjusts the first replicated index so that trades occur on announcement date rather than on effective date; and 3) a replication that delays trades by a 3- or a 12-month lag (which we call “lazy”) after a large portion of the mean reversion in price has taken place.
Actual S&P 500. Stocks in the index are weighted based on their market capitalization, adjusted for float to reflect the portion of the market capitalization available to the general public. This float adjustment was introduced in March 2005 and fully transitioned in September 2005, prompted by the growing number of new tech companies, which are closely held by their founders. Before this change the index weights were based on simple market capitalization, adjusted from time to time to allow for stock buybacks and secondary equity offerings.
Replicated S&P 500. We do not have precise daily data on the S&P 500 constituents and weights. We do have data on the component changes (i.e., the additions and deletions to the index), which we have collected from open sources such as Siblis Research (until March 2017) and Wikipedia (for the period April–December 2017). We begin our replication of the S&P 500 with a yearend 2017 snapshot of SPY ETF holdings. Then, using the history of component changes as a guide, we roll backward in time over the past 28 years to October 1989, periodically cross-checking the simulated holdings against the holdings of the SPY ETF (or the Vanguard 500, when SPY ETF holdings are not available to us). In our replication periods, as we roll back before September 2005, we shift from a weight based on the current-float-adjusted S&P 500 to a weight based on market capitalization.23
Of course, despite our efforts to match the original index, this replication procedure will still be imperfect. The most noteworthy sources of differences are 1) the lack of the exact index holdings and exact stock weights; 2) our rolling back from current float-adjusted weights, which do not track perfectly with the changes in the float between 2005 and yearend 2017; and 3) our use of market capitalization, unadjusted for the float information, when float information is unavailable, as we move from 2017 to 2005. That said, the replicated S&P 500 matches the actual S&P 500 with an R2 of 0.9997. The annualized performance since October 1989 differs from the published S&P 500 performance by a scant three basis points a year, and average annualized volatility is also within three basis points. It’s a pretty good match!
Replicated Trade-on-Announcement S&P 500. Before October 1989 the changes to the index were executed at the close of the announcement day. We wanted to know how the S&P 500 would have performed if it still followed this protocol. To gauge the performance impact of the grace period, we computed the replicated trade-on-announcement S&P 500 by modifying the replicated S&P 500 to have trading occur at the close of the announcement date instead of at the close of the effective date. Practically, no index fund could do this, but an index calculator certainly can, exactly as they did before October 1989. Of course, unless an investor has the private information from Standard & Poor’s on the exact announcements of additions and deletions, and their timing, this strategy cannot be replicated. Nevertheless, the exercise is still valuable for analytical purposes. The difference in performance between this index and the replicated S&P 500 is probably a useful, if crude, approximation of the trading costs actually experienced by index fund investors.
Lazy Replicated S&P 500. The actual S&P 500 buys stocks at lofty valuations and sells them at deeply depressed valuations. The index performance suffers as the prices subsequently revert to the mean. We simulated a lazy replicated S&P 500 that delays trades by several months (we show results for 3 and 12 months) after a large portion of the mean reversion in price has occurred. Delaying trading inevitably causes tracking error versus the actual S&P 500. Unlike the trade-on-announcement index, the lazy index is easy to implement and the difference in its performance versus the replicated S&P 500 captures the impact of mean reversion on index performance.24
Why Lazy Is Good for Index Fund Management!
We display the performance characteristics of the replicated S&P 500 indices from October 1989 through December 2017 in Table 7 as well as their dollar-growth paths relative to our replicated S&P 500 in Figure 6. Figure 6 graphically illustrates the efficacy of the simple approaches we explore to improve index fund results, the consistency of results, and the times when lazy strategies fail (notably, during growth-dominated bubbles).
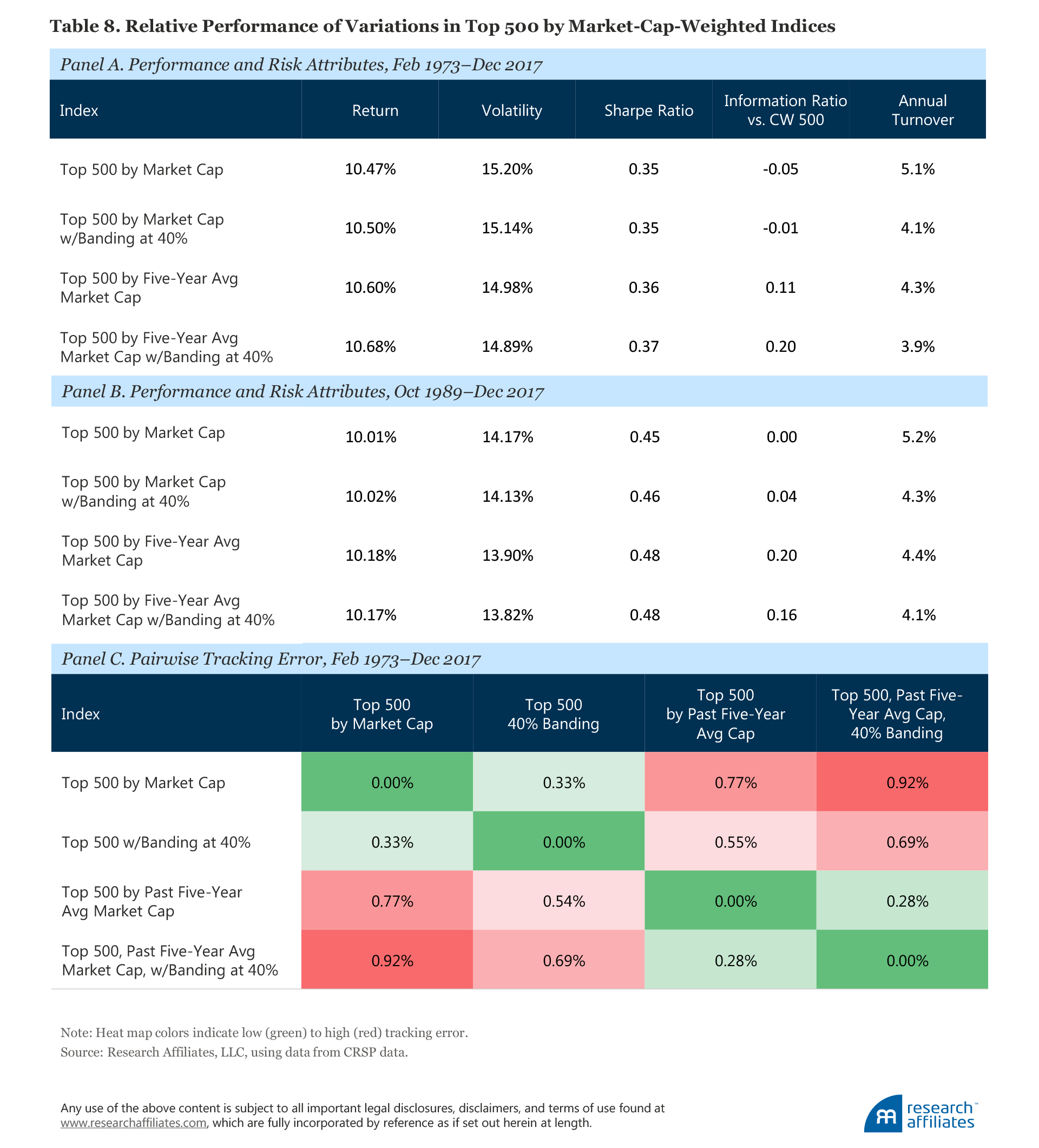
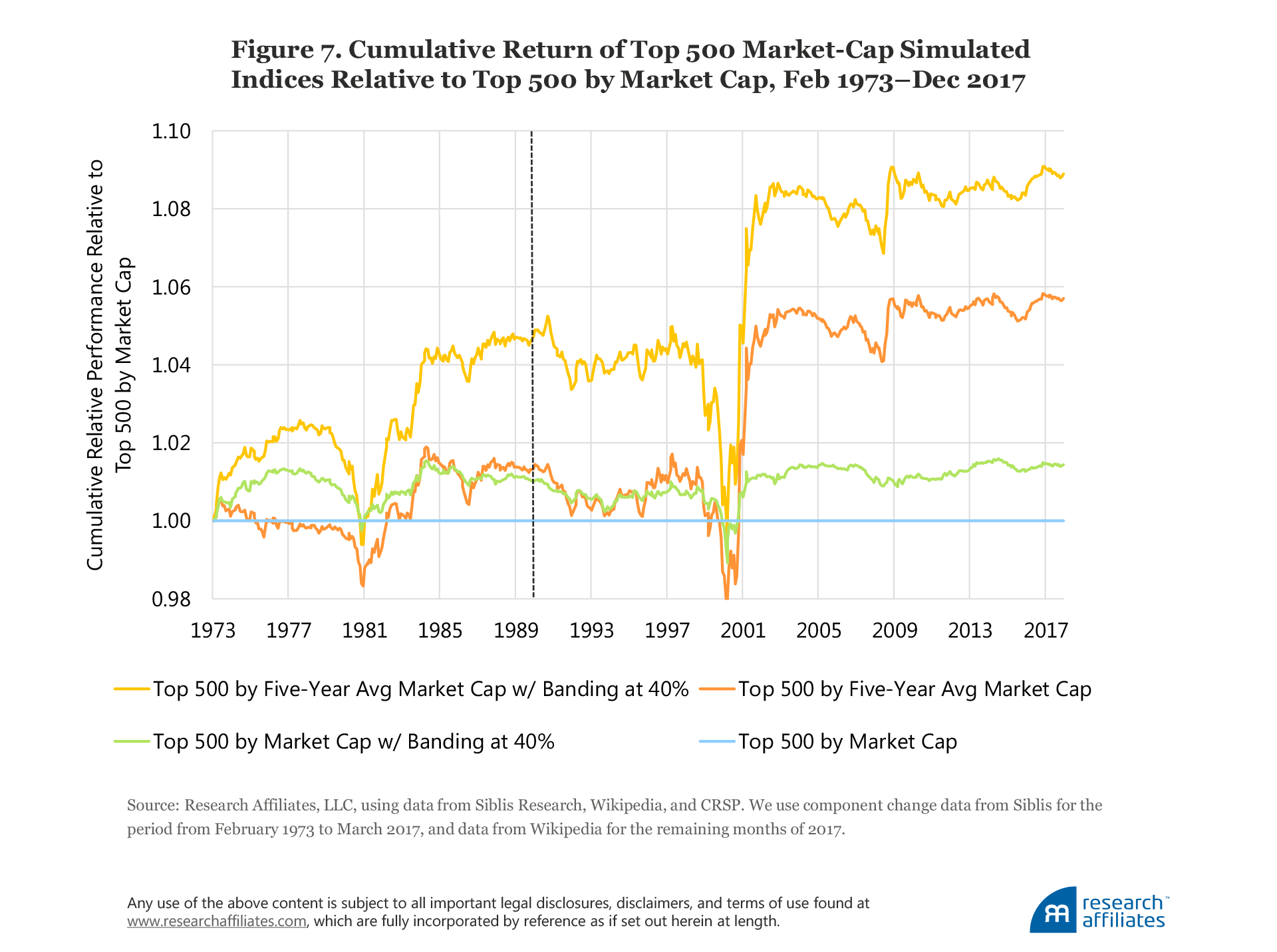
Figure 7 graphically shows the relative performance of these lazier cap-weight indices compared to the top 500 by market-cap portfolio. Although the gains are, of course, episodic, they are reasonably reliable on a rolling five-year basis, failing mainly during growth-dominated bubbles, such as in 1980 and in 1999.
Our work invites a question: Does the S&P Index Committee add value? From a pure return-and-risk perspective, maybe not, but we should not minimize the importance of comfort. The utility (in the academic finance meaning of the term) of having human involvement in the index construction, even with no difference in performance, may have value. Nevertheless, our research points to ways the S&P Index Committee can perhaps improve the performance of the index—through lower turnover and lower risk—which so many cap-weighted index fund managers are tracking!
Most studies of price impact document that transaction costs increase as the amount traded over a short period of time increases, and therefore implies that turnover-lowering techniques will reduce transaction costs.28 When both five-year averaging of market capitalization and banding are applied, the resulting portfolio outperforms both the top 500 by market-cap portfolio and the S&P 500 by 20–21 bps from February 1973 to December 2017, and lowers annual turnover for the same period to 3.9%, about 10% lower than S&P 500 turnover and about 25% lower than for the top 500 by market-cap portfolio. If the costs associated with the buy-high/sell-low dynamic and with turnover can be reduced by about 22–23 bps through reducing return drag, the associated total savings for the total of S&P 500 investors would be about $8.6 billion.29
When we delay index changes by 3 months and 12 months as in the lazy replicated S&P 500, portfolio turnover does not change. The other lazy strategies we analyze, however, such as using a smoothed five-year average market cap and 40% banding to avoid pointless churning as a stock soars onto the list and later tumbles off, are effective in lowering turnover and its associated costs. Figure 7 vividly illustrates the efficacy of this approach. With each additional step of averaging the past market cap to select stocks, banding to inhibit pointless trades, or both, we can add value while reducing risk.
In Tables 7 and 8, which present the performance and risk attributes of the alternative cap-weighted indices we analyze, an information ratio larger than 0.38 has statistical significance, and an information ratio larger than 0.52 has significance at the 99.9% level. Whereas delayed implementation exceeds this challenging threshold, as shown in Table 7, Panel A, a five-year smoothed market cap for selecting stocks and the application of banding do not rise to even the lower threshold, as shown in Table 8, Panels A and B. Consequently, the second two lazy options should be viewed as suggestive of possible ways to improve an index, but they do not rise to the level of statistically supporting the strategy.
Putting the Pieces Together
Investing in traditional cap-weighted indices has a negative impact on portfolio returns that arises from four sources: 1) the buy-high/sell-low dynamic of adding and deleting stocks in the index in which the newly large companies added to the index tend to be newly expensive and tend to mean revert downward in price after their addition, while the newly small companies deleted from the index tend to be newly cheap and tend to mean revert upward in price after their deletion; 2) the tendency for the top dogs (largest market-cap stocks in each sector or country) to underperform for protracted spans after achieving top-dog rank (and top-dog weight in the index funds!); 3) turnover, with all of its associated trading costs; and 4) index construction that chases the recently hot names rather than patiently reconstituting the index based on recent market cap, averaged over several years, and with banding to avoid the flip-flops.
We have shown that lazy trading up to a year after a change has been announced adds material and statistically significant alpha.
We have shown that the largest market-cap stocks in the world (and in any given sector or country) have disturbingly high odds of underperforming the world market (or sector or country), and that the magnitude of underperformance does not seem to dissipate over subsequent spans of as long as 10 years. Although it is highly unlikely an index fund would choose to eliminate Apple from its portfolio, a modestly lower weighting of sector and country top dogs should merit consideration, along with careful attention to the resulting tracking error.
We have shown that anticipating index changes is a worthwhile enterprise. Adding the performance spreads between additions and deletions made on both the day before a change in the index is announced and on the day after the effective date results in a performance spread of over 1,300 bps.
We have shown that lazy index construction, based on five-year average market cap and with banding to minimize the risk of flip-flops (additions that are quickly deleted), can materially improve performance, although tracking error increases relative to current indices. If the change in construction method was also made by the index providers, however, performance could be improved without index fund managers incurring any additional tracking error because the index itself changed!
We estimate that for index funds tracking the S&P 500, the return drag each year is around 36 bps from overreliance on sector top dogs, 25 bps from the buy-high/sell-low dynamic, 22 bps from transaction costs, and 21 bps from overly active index reconstitution. The average off-diagonal correlation of these “alphas” is a moderate 0.28 as shown in Table 9. Combining the four strategies adds roughly 100 bps in performance, but inflicts over 150 bps of tracking error.
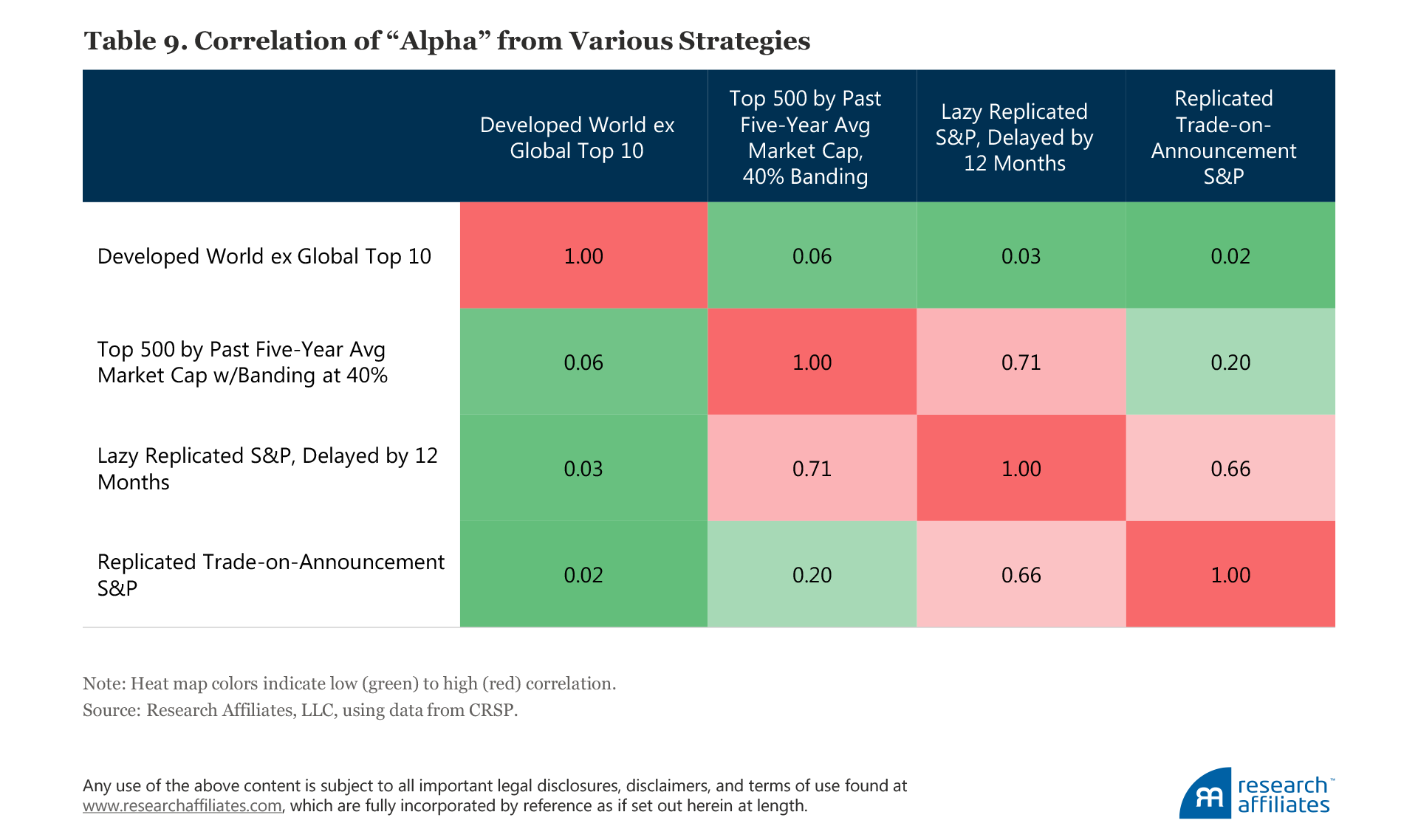
In our research into combining these strategies (acknowledging we are now straying deeper into data mining), we find about 15 bps of improved performance is easy to achieve, with just 25 bps of tracking error.30 Given that $4.1 trillion in assets tracks the S&P 500, this means those index fund investors could see approximately $6.2 billion in improved return every year. If these strategies add as much value in the future as in the past, value will be added in three of every four years and in 9 of 10 rolling five-year spans. Of course, if all index fund managers pursue these alpha sources, the alphas will disappear, but if a handful of scrappy indexers chooses to offer a “better” index, the opportunity will not be arbitraged away.
Conclusion
Sharpe (1991) asserted that the logic of traditional cap-weighted index fund investing relies on the assumption that “before costs, the return on the average actively managed dollar will equal the return on the average passively managed dollar.” This assertion, in turn, relies on a key assumption—that passive investors trade and hold the same collection of securities as the totality of active managers.
Unfortunately, in practice, this assumption does not hold for investors in the typical large-cap index funds. Quoting Berk and van Binsbergen (2015):
What Sharpe’s argument ignores is that even a passive investor must trade at least twice, once to get into the passive position and once to get out of the position. If we assume that active investors are better informed than passive, then whenever these liquidity trades are made with an active investor, in expectation, the passive investor must lose and the active must gain. Hence, the expected return to active investors must exceed the return to passive investors, that is, active investors earn a liquidity premium.
Berk and van Binsbergen, and others, are arguing that active managers, on average, should outperform passive managers by providing them with liquidity and by taking the other side of the indexers’ trade by buying the potentially undervalued stocks index funds sell and selling the potentially overvalued stocks index funds buy.
Our research supports this view by suggesting expedients which can help an index fund manager earn modest above-market returns by delaying portfolio changes—trading 3 to 12 months after the index is changed—and by deemphasizing the largest market-cap companies, which have disproportionate risk of future underperformance.
We argue that index providers (S&P, MSCI, FTSE, and so on) can construct better-performing indices that are less prone to chasing recent performance and that have lower turnover. In so doing, index providers would stop offering a free lunch to active managers. The use of five-year (or longer!) average market capitalization to identify the more stable and reliable top 500 or top 1,000 companies as well as the use of banding to inhibit flip-flop trades (stocks added to the index, which are quickly deleted) would almost entirely eliminate the buy-high/sell-low dynamic of standard large-cap portfolios and could also significantly reduce index fund turnover.
Our estimates suggest that a combination of these two changes in index construction can boost index fund performance by about 15 bps a year with only 25 bps of tracking error. In a world in which funds fight over fractions of a basis point in fees, this produces a material benefit!
Endnotes
1. The studies on S&P 500 reconstitution include Arnott and Vincent (1986), Harris and Gurel (1986), Goetzmann and Garry (1986), Shleifer (1986), Jain (1987), and Lamoureux and Wansley (1987).
2. Both the pre-announcement itself and the grace period (the time between the announcement date and the effective date) allow liquidity providers to gradually accumulate inventory of the stocks the index funds need to purchase on the effective date and to gradually absorb the stocks the index funds must sell; both lessen the price impact of the trading necessary to accomplish index rebalancing.
3. This observation is far less reliably true for other asset classes, in which uneconomic players can be startlingly large players. For instance, in investment-grade and sovereign bonds, central banks often trade without a profit motive, and insurance companies and banks have reserve haircuts that proactively encourage them to hold one class of bonds over another (e.g., creating a uneconomic sale of any newly downgraded junk bonds).
4. For more information, please see our “Alice in Factorland” article series composed of Arnott, Kalesnik, and Wu (2017a, b), Arnott, Clements, and Kalesnik (2017), and Arnott et al. (2017).
5. Bill Fouse at Wells Fargo Bank is often credited with running the first index funds in 1969, but this is not correct because his funds at the time excluded any company whose debt was below investment grade on the grounds of imprudence and violation of fiduciary standards. After 1973, Wells Fargo determined these exclusions led to material underperformance and began running true index funds.
6. According to ETFdb.com (http://etfdb.com/compare/lowest-expense-ratio/), today’s most competitive index-tracking ETFs are from Charles Schwab, with fees of three bps. Large segregated accounts that track indices for institutional clients may have management fees of one to two bps.
7. The CAPM was developed independently by Jack Treynor (1961, 1962), William Sharpe (1964), John Lintner (1965a,b) and Jan Mossin (1966). Their work built on earlier research by Harry Markowitz into diversification and modern portfolio theory. For their contribution to the economic sciences, Sharpe and Markowitz received, jointly with Merton Miller, the 1990 Alfred Nobel Memorial Prize in Economic Sciences.
8. Mean-variance efficiency means that the market portfolio, leveraged up or down to the desired risk level, is unbeatable except by luck.
9. De Bondt and Thaler (1981) demonstrated that 1) in the very short term (about a month after portfolio construction), the winner stocks underperform the loser stocks (this is known as short-term mean reversion and is partially explained by the bid–ask bounce as demonstrated by Roll, 1984); 2) in the intermediate term (up to a year), the winner stocks outperform the loser stocks (this is also known as the momentum effect documented first by Jegadeesh and Titman, 1993); and 3) in the longer term (two to three years), the winner stocks underperform the losers. Although the momentum effect moves in the opposite direction of short-term and long-term mean reversion, mean reversion dominates, as demonstrated by De Bondt and Thaler.
10. Banz (1981) showed that small-cap stocks outperform large-cap stocks. This phenomenon is known as the size premium. Berk (1997) argued theoretically and demonstrated empirically that the small-cap effect is largely driven by small-cap stocks being relatively cheaper and large-cap stocks being largely more expensive.
11. This is an oversimplification, of course. A high-yield stock might fall off the list, while delivering an above-market total return during the decade, and a low-yield stock can move onto the list while underperforming. And, the threshold for the top 10 list, as a percentage of the overall market capitalization, can change. Even so, it would be rare for a company to fall off the list while outperforming the market.
12. The 12 sectors are nondurables, durables, manufacturing, energy, chemicals, business equipment, telecom, utilities, shops, healthcare, finance, and other. Arnott and Wu (2012) used SIC codes to define the 12 sectors. These definitions may vary from the GICS definitions. The G-8 countries are Australia, Canada, France, Germany, Italy, Japan, United Kingdom, and United States.
13. Here’s a fun thought experiment. Suppose the S&P Index Committee had imagined their index might be used to run money. They would likely have considered other weighting schemes. Weighting by market capitalization would likely have been dismissed as preposterous: Why weight a company more heavily just because it’s more expensive? Perhaps weighting by a company’s sales would have carried the day. Well, we would then have trillions fundamentallyindexed today, with cap-weight strategies barely registering. A marketer for a cap-weight index fund might be heard to say: “Nevermind that it loses 75% in rolling five-year spans. In theory, you can’t beat cap weight on a risk-adjusted basis.”
14. According to the S&P Dow Jones Indices “Annual Survey of Assets” as of yearend 2016, $2.95 trillion in total assets were indexed to the S&P 500. According to the prior year’s survey, the yearend 2015 assets indexed to the S&P 500 totaled $2.14 trillion. Net of 12% price appreciation in 2016, this would imply $550 billion net inflows into the S&P 500 tracking funds during 2016. If we add 20% for price appreciation of the S&P 500 in 2017, and add the same flows experienced in 2016, then the $2.95 trillion should have grown to approximately $4.1 trillion by yearend 2017.
15. 2 x 4.4% x $4.1 trillion = $360 billion.
16. According to the S&P Dow Jones Indices “Annual Survey of Assets” as of yearend 2016, $5.7 trillion in assets were benchmarked to the S&P 500 (excluding directly indexed assets). According to yearend 2015 estimates, S&P 500-benchmarked assets equaled $5.4 trillion. Given the 12% price appreciation in 2016, the benchmarked assets likely experienced an outflow of $0.35 trillion. If we assume 20% price appreciation in 2017 and a similar level of outflow as in 2016, we estimate the benchmarked assets to be around $6.5 trillion.
17. The raw component change list from Siblis Research includes company names, tickers, action of the change (addition or deletion), announcement date, and effective date. We use component change data from Siblis for the period from March 1973 to March 2017, and data from Wikipedia for the remaining months of 2017.
18. The number of constituents in the S&P 500 is not always 500. Since 2015, the index has held 505 stocks following a methodology change to allow multiple share classes of S&P 500 constituent companies.
19. Additions lacking price data in the six months before the effective date will be assumed to be nondiscretionary, and deletions missing price data for the six months after the effective date will be assumed to be nondiscretionary. This rule will not pick up recent IPOs as nondiscretionary additions because, according to the S&P rule book, an IPO is required to have at least 12 months of history to be eligible for consideration for S&P inclusion. https://us.spindices.com/documents/methodologies/methodology-sp-us-indices.pdf
20. The valuation discount is defined as the valuation ratio of the stock relative to the market valuation ratio. With the exception of P/B, for which we use single-year book value, we use five-year-average fundamental values in the other price-to-fundamentals ratios: P/E, P/CF, P/S, and P/D. The average valuation discount is the exponent of the pooled average of the log of the valuation discount ratio for each individual metric. The total average is the simple average of the four.
21. This asymmetry is consistent with the findings by Chan, Kot, and Tang (2013) who found a permanent positive effect on the stock price from being included in the S&P 500. The authors attributed the effect to likely broader coverage by analysts, higher liquidity, and more institutional ownership.
22. Another reason the glamour stocks may have been added to the S&P 500 may have been to minimize order imbalances and volatility due to increased orders from index funds.
23. For periodic cross-checking, we use SPY ETF holdings from December 2010 and September 2005 (when the S&P 500 fully transitioned to float-adjusted weighting). We use Vanguard 500 holdings as of December 1999. The holdings data are from Bloomberg.
24. Arnott, Beck, and Kalesnik (2015) found that a portfolio using 20-year-old stale capitalization weights outperforms an index using current information by about 180 bps a year.
25. Attentive readers may surmise that if discretionary deletions outpace additions by over 20% in the first year after an index change takes effect, and with average turnover of over 4% a year, the lazy replication should add over 80 bps a year. Correct? Not really. Remember that additions are far larger (3½ times the valuation multiples on larger sales and profits) than deletions, so additions are over 4% a year. Deletions are far smaller, with the difference made up of lightly trimming all remaining S&P 500 constituents to complete the 4% in purchases. The additions lag the S&P 500 by 1.28% in the year after addition, which contributes 5–6 bps of the 25 bps in alpha generated from laziness. If discretionary deletions are less than half of all deletions, and if they are half the size of the additions, then they represent only about 1% of annual turnover (and a little less for the Russell 1000 and Russell 3000). If they outperform by 19% in the year after they have been deleted, this adds 19 bps of additional benefit from laziness.
26. Our test starts in 1973, the first year NASDAQ-traded stocks are captured in the CRSP/Compustat database. Thus, the turnover beginning in 1973 originates predominantly from index dynamics.
27. This approach sometimes leads to having more stocks to add than to drop, and vice versa. If, for example, we need to add 20 stocks and drop 30, we choose to drop the 20 smallest, and vice versa, so that the index remains a 500-stock index.
28. The same finding also implies that the commonly used approach of rebalancing on a single day of the year is flawed.
29. If we take the difference in performance of 22 bps between the replicated trade-on-announcement S&P 500 and the replicated S&P 500 as the measure of explicit trading costs, reducing this by 10% would translate into 2 bps a year of better performance. Adding up these 2 bps of savings from lower trading costs and the 20–21 bps of savings from removing the buy-high/sell-low dynamic translates into about 22–23 bps of savings.
30. Granted, we are venturing into the realm of data mining, but we find that when the following three strategies are combined in proportions of 1:1:3, approximately 14 bps of value is added with 25 bps of tracking error: global world ex top 10 global stocks, lazy replicated S&P 500 delayed by 3 months, and lazy replicated S&P 500 delayed by 12 months. If we add the replicated trade-on-announcement S&P 500 as the fourth driver of return (which is not easy to reliably replicate, but can be roughly approximated) and assign weights in the proportions of 1:1:3:13, with the last weight of 13 given to the replicated trade-on-announcement S&P 500 strategy—the value-add is 18 bps with tracking error of 25 bps. Giving the 18 bps a haircut to account for the fact that without private information a total replication of the replicated trade-on-announcement S&P 500 is impossible, we arrive at a value-add of 15 bps.
References
Arnott, Robert, Noah Beck, and Vitali Kalesnik. 2015. “Rip Van Winkle Indexing.” Journal of Portfolio Management, vol. 41, no. 4 (Summer):50–67.
Arnott, Rob, Mark Clements, and Vitali Kalesnik. 2017. “Why Factor Tilts Are Not Smart ‘Smart Beta.’” Research Affiliates Publications (May).
Arnott, Rob, Vitali Kalesnik, Engin Kose, and Lillian Wu. 2017. “Can Momentum Investing Be Saved?” Research Affiliates Publications (October).
Arnott, Rob, Vitali Kalesnik, and Lillian Wu. 2017a. “The Folly of Hiring Winners and Firing Losers.” Research Affiliates Publications (September).
———2017b. “The Incredible Shrinking Factor Return.” Research Affiliates Publications (April).
Arnott, Robert D., and Stephen J. Vincent. 1986. “S&P Additions and Deletions: A Market Anomaly.” Journal of Portfolio Management, vol. 13, no. 1 (Fall):29–33.
Arnott, Rob, and Lillian Wu. 2012. “The Winner’s Curse.” Journal of Indexes (October 29).
Banz, Rolf W. 1981. “The Relationship between Return and Market Value of Common Stocks.” Journal of Financial Economics, vol. 9, no. 1 (March):3–18.
Berk, Jonathan B. 1997. “Does Size Really Matter?” Financial Analysts Journal, vol. 53, no. 5 (September/October):12–18.
Berk, Jonathan B., and Jules H. van Binsbergen. 2015. “Measuring Skill in the Mutual Fund Industry.” Journal of Financial Economics, vol. 118, no. 1 (October):1–20.
Blitzer, David. 2014. “Inside the S&P 500: An Active Committee.” Indexology® Blog, S&P Dow Jones Indices (August 7).
Chan, Kalok, Hung Wan Kot, and Gordon Y.N. Tang. 2013. “A Comprehensive Long-Term Analysis of S&P 500 Index Additions and Deletions.” Journal of Banking and Finance, vol. 37, no. 12 (December):4920–4930.
Chen, Honghui, Gregory Noronha, and Vijay Singal. 2004. “The Price Response to S&P 500 Index Additions and Deletions: Evidence of Asymmetry and a New Explanation.” Journal of Finance, vol. 59, no. 4 (August):1901–1930.
De Bondt, Werner F.M., and Richard Thaler. 1985. “Does the Stock Market Overreact?” Journal of Finance, vol. 40, no. 3 (July):793–805.
Goetzmann, William, and Mark Garry. 1986. “Does Delisting from the S&P 500 Affect Stock Price?” Financial Analysts Journal, vol. 42, no. 2 (March/April):64–69.
Harris, Lawrence, and Eitan Gurel. 1986. “Price and Volume Effects Associated with Changes in the S&P 500 List: New Evidence for the Existence of Price Pressures.” Journal of Finance, vol. 41, no. 4 (September):815–829.
Jain, Prem. 1987. “The Effect on Stock Price from Inclusion In or Exclusion From the S&P 500.” Financial Analysts Journal, vol. 43, no. 1 (January/February):58–65.
Jegadeesh, Narasimhan, and Sheridan Titman. 1993. “Returns to Buying Winners and Selling Losers: Implications for Stock Market Efficiency.” Journal of Finance, vol. 48, no. 1 (March):65–91.
Lamoureux, Christopher, and James Wansley. 1987. “Market Effects of Changes in the Standard & Poor’s 500 Index.” Financial Review, vol. 22, no. 1 (February):53–69.
Lintner, John. 1965a. “The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets.” Review of Economics and Statistics, vol. 47, no. 1 (February):13–37.
———. 1965b. “Security Prices, Risk, and Maximal Gains from Diversification.” Journal of Finance, vol. 20, no. 4 (December):587–615.
Lynch, Anthony, and Richard Mendenhall. 1997. “New Evidence on Stock Price Effects Associated with Changes in the S&P 500 Index.” Journal of Business, vol. 70, no. 3 (July):351–383.
Mossin, Jan. 1966. “Equilibrium in a Capital Asset Market.” Econometrica, vol. 34, no. 4 (October):768–783.
Roll, Richard. 1984. “A Simple Implicit Measure of the Effective Bid–Ask Spread in an Efficient Market.” Journal of Finance, vol. 39, no. 4 (September):1127–1139.
Sharpe, William F. 1964. “Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk.” Journal of Finance, vol. 19, no. 3 (September):425–442.
———. 1991. “The Arithmetic of Active Management.” Financial Analysts Journal, vol. 47, no. 1 (January/February):7–9.
Shleifer, Andrei. 1986. “Do Demand Curves for Stocks Slope Down?” Journal of Finance, vol. 1, no. 3 (July):579–590.
Treynor, Jack. 1961. “Market Value, Time, and Risk.” (August 8). Available on SSRN.
———. 1962. “Toward a Theory of Market Value of Risky Assets.” (Fall). Available on SSRN.

