
Market impact trading costs arise from buying and selling securities at temporarily impacted prices during index rebalances.
These costs are not easily observed because they simultaneously occur in the index and the index tracking portfolio.
The growth in smart beta investing may erode these strategies’ future returns as they reach investment capacity, which is inversely related to annual trading costs.
Investors should consider a strategy’s cost-driving characteristics, such as turnover, concentration, liquidity, and total AUM, when making investment decisions.
Management fees and commissions are hardly the only costs an investor needs to consider. We quantify the price impact created from buying and selling stocks when rebalancing index-tracking equity portfolios, and find the impact can significantly erode the expected excess returns of indexing strategies.
Because most index-tracking managers trade in unison when the index rebalances, the prices of stocks they buy are temporarily inflated, and those they sell are temporarily depressed. As prices revert in the days following the rebalance, investors lose money. Market impact is a very real trading cost, but is hidden from the investor because the portfolio’s value changes simultaneously with the index’s. A better understanding of how indices are designed can help investors select those with the greatest potential to deliver excess return net of realistic market impact costs.
The Double-Edged Sword of Smart Beta’s Popularity
With transparent investment processes, a relatively low management fee, and the potential for above-average performance, smart beta strategies have diverted a large portion of assets away from traditional active management.
According to data from Morningstar Direct, the assets under management (AUM) of smart beta ETFs and mutual funds in global markets increased from just below $75 billion in 2005 to more than $800 billion by the end of 2016. The growth would be even higher if we included the smart beta assets held directly by institutional investors.
But investors may not be consistently well served by the financial services industry’s success in gathering smart beta assets. Other researchers have shown that fund size is inversely related to performance. As the amount of AUM rises, managers must buy more of the stocks in their opportunity set, creating upward price pressure that lowers the expected return. Conversely, when managers sell existing positions, their trading pushes prices down, reducing the realized return.
Moreover, index-based smart beta strategies are not exempt from the return-dampening effect of trading costs. When a provider rebalances an index, all the managers tracking it enter the market to adjust their positions accordingly. The large volume of buy and sell orders for the same securities, executed at the same time, results in securities prices moving against the managers, producing losses for the funds’ investors.
These market impact costs are not easily observed. The fact that a fund’s net asset value moves in parallel with the index return creates the illusion that the portfolios have no market impact. Nonetheless, the cost is reflected implicitly in both the index and the tracking funds, whose values change simultaneously with the prices of their holdings. The returns of both are lower than they would have been in the absence of trading.
Estimating smart beta transaction costs—in particular, the “hidden” market impact costs—can help market participants see how much they matter. Understanding what drives them may help managers to design strategies more efficiently and investors to choose strategies more knowledgeably. Investors typically focus their attention on simulated or actual performance—which is often not even helpful information—and on explicit fees and expenses, often the smallest part of the cost. As a result, the importance of thoughtful product design is commonly underappreciated. Yet transaction costs are more persistent than performance, which tends to revert to the mean. Transaction costs, reaching to scores of basis points, can have far more impact than the management fee on the investor’s realized rate of return.
Introducing the Study
Our study has two phases. First, to unmask the market impact costs that arise from synchronous buying and selling, we develop a simple regression model enabling us to analyze the behavior of stocks that were traded during the rebalancing of 49 FTSE RAFI™ indices, a family that includes some of the longest live histories in the smart beta space. We quantify the abnormal price change that was unexplained by regional market and industry excess returns and find a pattern of adverse movements on the trade date and partial reversals over subsequent trading days.
Second, to compare the capacities of popular smart beta strategies, we apply a linear market impact cost model (Aked and Moroz, 2015) to simulated indices. The construction methodologies are available on our website’s Smart Beta Interactivetool. We backtest the strategies, approximate their costs at a given level of AUM, identify their cost drivers, and estimate the US dollar amount of assets each strategy can hold without exceeding an arbitrary, but uniform, threshold of 50 basis points (bps) in annual market impact costs.
Estimating Market Impact Costs
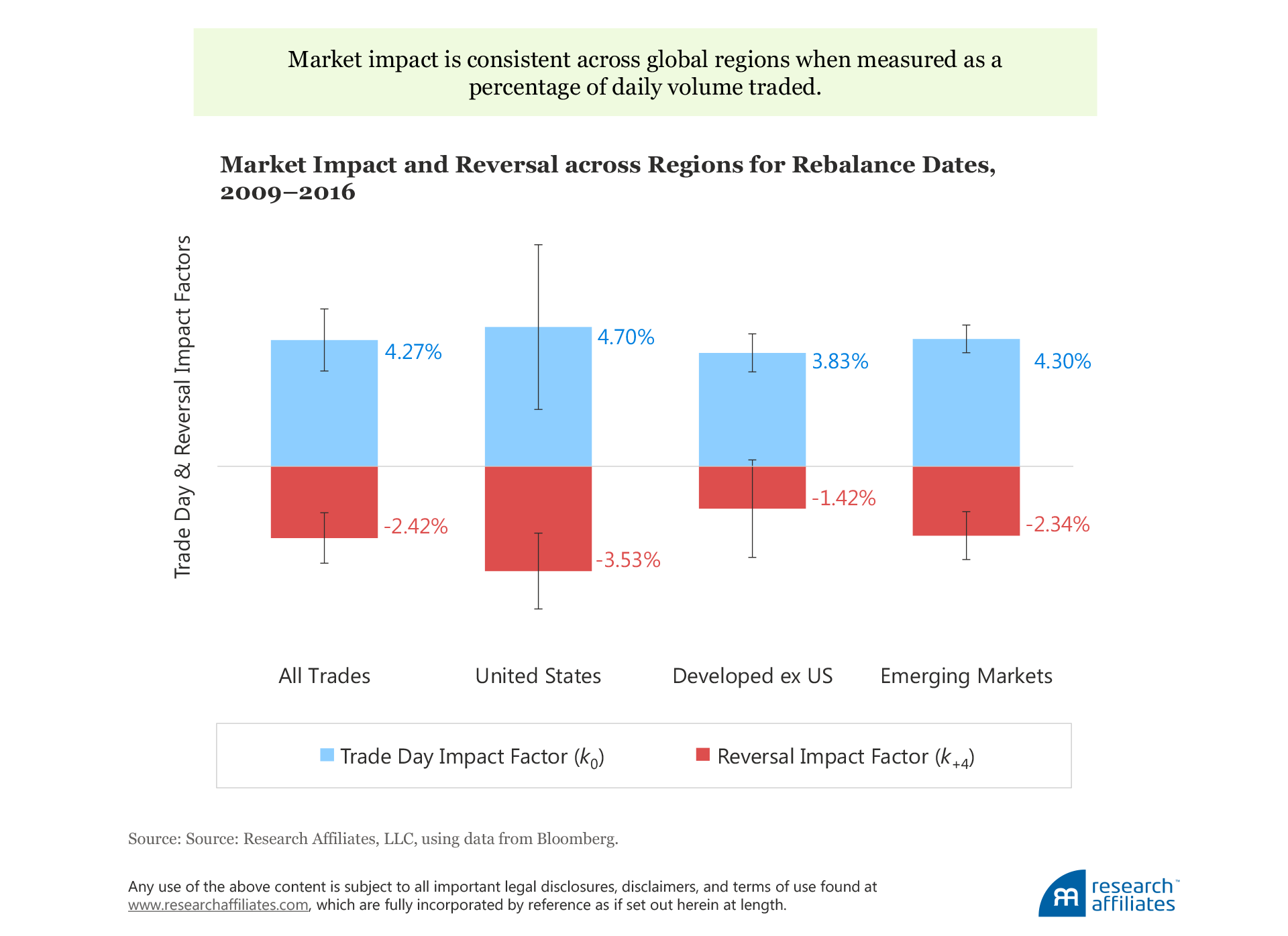
For each of the 49 FTSE RAFI indices in our study, we use the aggregate AUM and the changes in security weights as of rebalance dates from 2009 to 2016. The dollars traded in each stock in each index is the product of the amount of AUM tracking the index and the weight change of the stock from the close of the rebalance date (pre-rebalance weight) to the open on the next trading day (post-rebalance weight). Because the same stock can be traded by multiple indices, we aggregate the dollars traded for each stock across all indices to determine the total dollars traded. Thus our data, totaling nearly 50,000 transactions valued at more than $56 billion, reflect all the rebalancing trades by all the managers tracking the indices over the study period.
With these data in hand, we obtain a stock’s residual return through regressing its local-currency stock return against its corresponding market and industry returns centered on the trade date. We ascribe the residuals to an event common to all companies—the fact they are all traded heavily on the index rebalancing date—along with other events that roughly cancel one another because they are idiosyncratic to each company. Then, in a panel regression using all of the trades, we isolate the trade-day market impact factor, k0, the excess return that is linearly related to the size of the rebalancing trade relative to the stock’s total trade volume on the rebalance day.
Our research confirms that the magnitude of price impact is predictable because it is directly related to the size of the trade and the security’s liquidity. Strategies incur approximately 30 bps of trading costs due to market impact for every 10% of a stock’s average daily volume traded in aggregate. Significant evidence of a pattern that holds across global markets also comes to light: a market impact of 43 bps, on average, on the rebalance day, with partial reversal over the next four days. Our analysis, over the period 2009–2016 of the US market, developed markets excluding the United States, and emerging markets, indicates that for every 10% of volume traded in a stock, the price changes 43 bps, on average, against the trade on the trade day, and 24 bps in the other direction over the next four days.
We offer a hypothetical example to illustrate how the market impact occurs as a trading cost to investors. Suppose a trader executes a round-trip trade (buy, hold, and sell) of a stock with a market value of $100 per share at a trade size equivalent to 10% of daily trading volume. He observes a price level at $100, and buys the stock at an average price of $100.43. After a few days, the value of the stock depreciates by 24 cents, on average, to $100.19. The trader then places a sell order on the stock, at which point the price moves down by 43 cents, on average, and he sells at $99.76. In total, the trader loses 67 cents per share, on average ($100.43 minus $99.76), or 67 bps for the round trip. A few days after the sale, the price of the stock reverts 24 cents, on average, to $100, with the result being no long-term impact from trading on the price.
Managers who submit their orders around the time the market closes may have low tracking errors against the indices they target. However, the managers’ trades push stock prices up or down, and the impact is embedded in the returns of the indices, whose value, after all, is calculated on the basis of closing prices. This is an important point. The market impact cost is hidden and cannot be seen in a direct comparison of fund performance and index performance.
Comparing Smart Beta Strategies
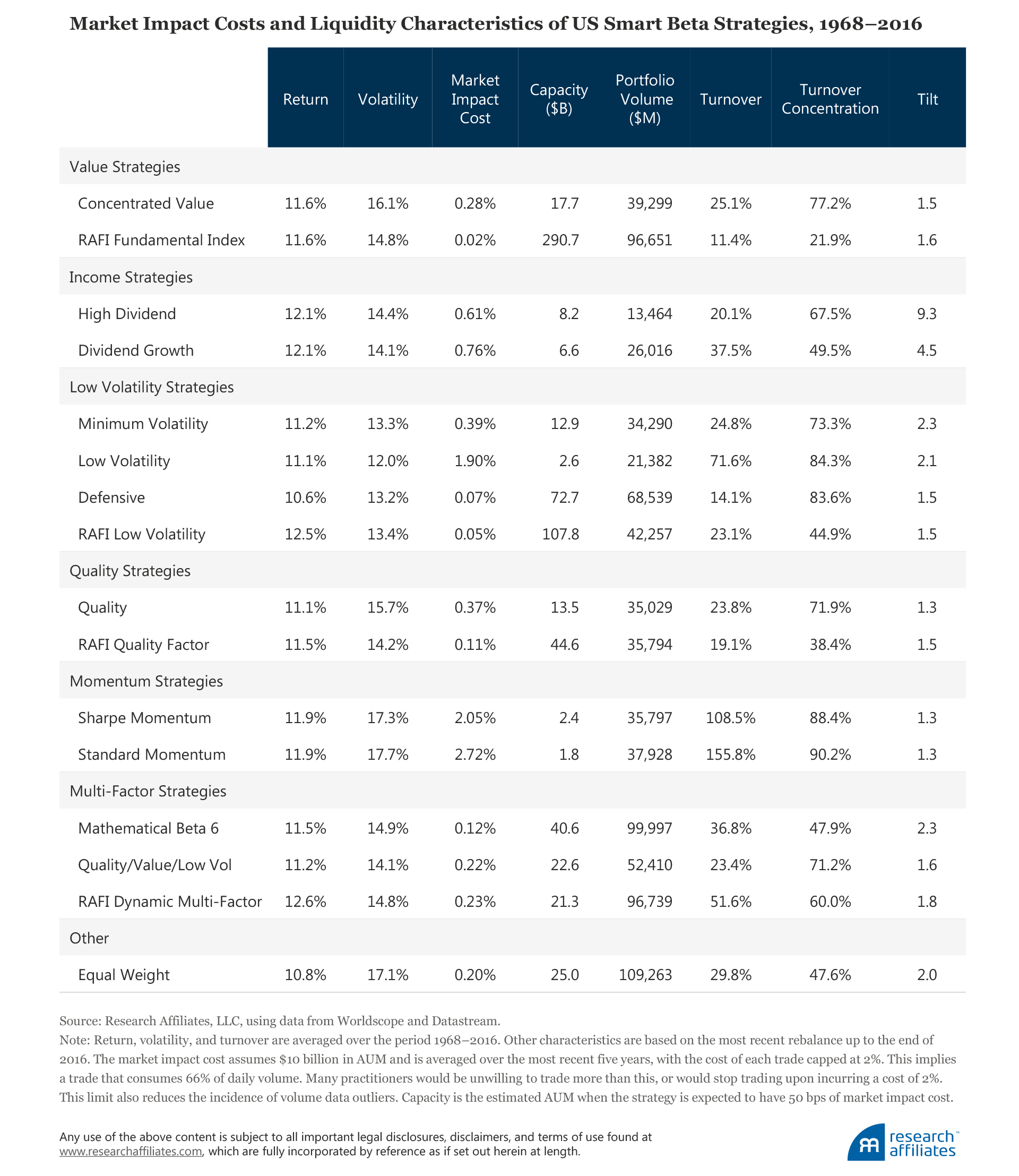
We also estimate the costs associated with implementing a range of smart beta strategies; the appendix summarizes the smart beta methodologies we use. These methodologies are intended to simulate the more popular strategies in the marketplace today. We design the methodologies to provide consistent starting universes, regional definitions, and rebalance dates. For calculating costs, we assume AUM equal to $10 billion for US and international strategies, and AUM equal to $1 billion for emerging-market strategies.
Our findings are striking. We determine, for example, that over the period we observe, momentum strategies with as little as $10 billion in aggregate assets have trading costs of 200 bps or more. At the same level of AUM, income strategies’ costs are in the 60–80 bps range, and quality strategies’ costs fall below 40 bps.
The comparisons are even more meaningful if we understand the factors that drive different strategies’ very different costs. Applying Aked and Moroz’s market impact cost model allows us to attribute implementation costs to the smart beta strategies’ key trade-related characteristics, including portfolio volume, tilt, turnover, turnover concentration, and number of trading days. We define and describe these terms as follows:
1. Portfolio volume is the aggregation of median daily trade volume, in dollars, of all the stocks in the portfolio. A strategy’s cost is inversely proportional to its portfolio volume; all else equal, a small-cap portfolio would cost twice as much to implement as a large-cap portfolio if it has half the latter’s aggregate volume.
2. Tilt, in this context, is the degree to which the portfolio holding weights deviate from a volume-weighted portfolio, which is the most liquid combination of a given set of stocks. The volume-weighted portfolio has a tilt of 1. Holding all else equal, a portfolio with a tilt of 2 would experience twice-as-high market impact costs.
3. Annual one-way turnover is another determinant of cost; in general, a strategy that requires a higher rate of trading incurs higher market impact costs.
4. Turnover concentration reflects the degree to which trades are spread across the portfolio. Consider, for example, two rebalances with the same turnover rate. One requires buying $100 million of one large-cap company’s shares, while the other requires buying $10 million worth of the shares of 10 large-cap companies. Highly concentrated trades, such as the former, are more costly to execute. Additionally, strategies that rebalance more frequently (e.g., quarterly versus annually) will tend to have lower turnover concentration.
5. Number of trading days is also an important factor in cost, but note that it describes execution rather than being a characteristic of a smart beta strategy. An implementer less concerned with tracking error can effectively lower the cost by spreading a single rebalance through multiple days of market liquidity.
Solid cost estimates can additionally shed light on relative capacities. Procedurally, we set a fixed cost for all strategies at 50 bps a year and compute the corresponding AUM, effectively defining capacity as the largest amount of assets a strategy can hold without incurring more than 50 bps of market impact cost a year. This approach gives us an even basis for comparing the capacities of different smart beta strategies.
The market impact costs of the simulated US smart beta strategies we study range from a high of 272 bps for a standard momentum strategy to a low of 2 bps for the Fundamental Index™ strategy. Inversely, the capacities of these strategies, at a uniform 50 bp cost level, run from a low of $2 billion for a standard momentum strategy to a high of $291 billion for a Fundamental Index strategy.
The portfolio statistics are telling. For instance, the Sharpe momentum and standard momentum strategies have high turnover rates (108.5% and 155.8%, respectively), high turnover concentrations (88.4% and 90.2%, respectively), and low portfolio volumes ($35.7 billion and $37.9 billion, respectively) relative to the other smart beta strategies. Collectively, these characteristics imply that these two strategies have concentrated or illiquid holdings, completely trade out of and into a few positions, and do so at a fast pace. All of these traits contribute to the strategies’ high cost of implementation. In contrast, Sharpe momentum and standard momentum have the lowest tilt, at 1.3, which suggests their weighting by market capitalization (or a variant) mitigates some of the trading challenges. Overall, momentum may not be a good choice as a stand-alone smart beta strategy, assuming implementers apply passive execution.
The high dividend and dividend growth strategies also have fairly high costs. Their turnover rates are much lower than those of the momentum strategies because they both employ stringent banding rules. The main causes of their high costs are their low portfolio volumes of $13.4 billion and $26.0 billion, respectively, and high tilts of 9.3 and 4.5, respectively, likely the result of investing in a small number of the highest-yielding companies and weighting their positions on the basis of yield. Investors who seek a steady stream of healthy dividends pay a hidden price in the form of market impact costs.
The Fundamental Index is a broad market index, as indicated by its very high portfolio volume of $96.6 billion. Its rebalancing primarily consists of restoring existing constituents to their fundamental weights. Accordingly, both its turnover rate (11.4%) and turnover concentration (21.9%) are the lowest among the smart betas strategies in our sample. Its tilt is also low, on a par with cap-weighted strategies, suggesting that fundamental size is highly correlated with trading volume. In contrast, the concentrated value strategy has significantly lower capacity. A strong and straight bet on a target factor may not necessarily lead to a higher return, and almost certainly creates higher implementation costs as well as more risk.
Although the strategies in the low volatility group have distinctive methodologies and characteristics, they all achieve their primary investment objective—respectable returns with lower risk. They have strikingly different market impact costs, however, ranging from 1.9% for the basic low volatility strategy (almost as high as momentum) to 7 bps for the defensive strategy and 5 bps for the RAFI Low Volatility strategy (almost as low as the Fundamental Index). The extended high–low range underlines the importance of index design. The basic low volatility strategy has the simplest methodology and the lowest simulated volatility. Nevertheless, a 185 bp difference in expected implementation costs seems too great to overlook.
Finally, the multi-factor strategies have moderate costs despite their added complexity. Mixing multiple single-factor portfolios tends to reduce costs because the constituent strategies find liquidity in different subsets of the market, and the trades occurring at the individual factor level may offset one another at the portfolio level.
In Closing
Given the increasing roster of smart beta strategies and assets under management, trading costs are an increasingly important consideration. Too many investors focus attention on a few basis-points difference in fees, while ignoring trading cost differences that can be 100 bps or more. When we better understand implementation costs in relation to strategy characteristics, providers can offer, and investors can select, smart beta funds with better long-term net-of-cost returns. Given a strategy’s specific investment objective, some undesirable characteristics are admittedly unavoidable. For example, momentum strategies inherently come with high turnover rates, and dividend-yield strategies entail high concentrations. Nonetheless, careful design can potentially reduce market impact. Such techniques include rebalancing in multiple tranches, executing only strong-conviction trades in order to limit turnover, and weighting stocks by a metric correlated with their liquidity.
Reference
Aked, Michael, and Max Moroz. 2015. “The Market Impact of Passive Trading.”Journal of Trading, vol. 10, no. 3 (Summer):5–12.
Appendix: Smart Beta Simulation Methodologies
1. Concentrated Value: The semi-annually rebalanced strategy selects the top 20% from the Large + Mid Cap universe based on a value score calculated using the ratios of price to book value, price to earnings, and enterprise value to cash flow from operations. It weights selections by market capitalization times value score.
2. RAFI™ Fundamental Index™: The strategy selects and weights companies according to four fundamental measures of company size: book value, cash flow, dividends plus buybacks, and adjusted sales. It is implemented in four annually rebalanced tranches such that trades are spread over four quarters.
3. High Dividend: After screening for dividend growth and dividend coverage, the annually rebalanced strategy selects 100 stocks by dividend yield from the Large + Mid + Small Cap universe, and weights selections by indicated dividend yield.
4. Dividend Growth: For US market simulations, the strategy rebalances quarterly, selecting companies from the top 1,500 by market cap that had stable or increasing dividends in the last 20 years. For developed-market simulations, stocks with stable or increasing dividends in the last 10 years are selected from the Large + Mid + Small Cap universe, and weighted by indicated dividend yield. In emerging market simulations, stock selections are made based on growing earnings and high dividend yields, and weighted by annual dividend yield. Developed and emerging markets are rebalanced semi-annually.
5. Minimum Volatility: The strategy minimizes the volatility of a large- and mid-cap portfolio by means of a constrained optimization. Constraints include maximum single-holding weight, country and sector active weights, and turnover limits. The optimization is recomputed semi-annually.
6. Low Volatility: The quarterly rebalanced strategy selects the 20% lowest-volatility stocks from the parent universe and weights them by 1/volatility.
7. Defensive: The strategy reweights stocks from the parent universe according to a stability score, which captures low volatility, low earnings variability, low leverage, and high return on assets. The portfolio is rebalanced annually.
8. RAFI Low Volatility: The strategy selects companies from each sector and region of the parent universe with low valuations and low systemic risk, and weights selections by their fundamental size. It is implemented in four annual rebalancing tranches such that trades are spread over four quarters.
9. Quality: The semi-annually rebalanced strategy selects companies from the Large + Mid Cap parent universe based on a quality score that combines high return on equity, low debt to equity, and low earnings variability, and weights selections by market capitalization times quality score.
10. RAFI Quality Factor: The strategy selects the top 25% of large companies with high profitability and low investment, and weights selections by fundamental size. It is implemented in four annual rebalancing tranches such that trades are spread over four quarters.
11. Sharpe Momentum: The strategy selects companies from the Large + Mid Cap parent universe based on a momentum score reflecting prior 6-month and 12-month Sharpe ratios, and weights selections by market capitalization times momentum score. It is rebalanced semi-annually, with additional rebalances triggered by volatility spikes.
12. Standard Momentum: The quarterly rebalanced strategy selects the top third of companies from the Large + Mid Cap parent universe by momentum, defined as prior-year return, skipping the most recent month, and weights selections by market capitalization.
13. Mathematical Beta 6: The quarterly rebalanced strategy equally weights six factor indices: value, momentum, mid-cap, low volatility, profitability, and investment. Each factor is constructed by selecting half the companies from the regional large-cap universes by characteristics, and weighting the selections via five diversification methods.
14. Quality/Value/Low Vol: The fund equally weights the quality, minimum volatility, and a value strategy that reweights the Large + Mid Cap parent universe by fundamental size.
15. RAFI Dynamic Multi-Factor: At every quarter, the strategy dynamically weights five factor indices—value, low volatility, quality, momentum, and size—based on long-term reversal and short-term momentum. The large size factor is constructed by selecting the top 25% of the Large + Mid Cap universe (50% for momentum), weighting selections by fundamental size (by market capitalization for momentum). The small size factor is constructed by equally weighting the other four factors constructed within the small company universe.
16. Equal Weight: The quarterly rebalanced strategy equally weights all stocks in the parent universe.

