We show that factors constructed from fundamental characteristics have earned high returns, while those constructed from statistical betas have earned returns close to zero.
By choosing investment strategies to intentionally create exposure to factor betas, investors may be gaining exposure to uncompensated risks.
When designing factor-based investment strategies, investors should seek exposure to the fundamental characteristics that define a factor and use statistical measures of factor betas to manage factor risks.
Seeking to obtain exposure to factor betas is a misguided means to obtain the returns available from factor investing.
When choosing among factor investing strategies, investors benefit from understanding the key difference between the two principal ways of measuring factor exposures: characteristics and betas. Characteristics measure the fundamental tilts of a portfolio by aggregating financial metrics including value measures such as price-to-book and price-to-earnings ratios; profitability measures such as earnings-to-book and earnings-to-assets ratios; and momentum measures defined by stock price trends. Betas measure the co-movement of the returns of a strategy and predefined factor portfolios. We find that characteristics are better predictors of returns, whereas betas are better providers of information useful for managing factor risks.
The characteristics-based approach follows fundamental investment principles supported by empirical evidence that demonstrates factors provide persistent sources of return premia. The beta-based approach of measuring factor exposures follows the theoretical argument that these factor premia exist to compensate for exposure to factor risks. These two approaches, however, are not mutually exclusive. Because both characteristics and betas likely represent incomplete proxies for underlying factor exposures, each provides information complementary to the other.
Characteristics directly measure fundamental factor exposures and thus better predict future returns. Portfolios constructed using characteristics information create exposures to factor risks. By measuring return co-movements, betas provide investors information useful in the management of these factor risks.
To inform investors about the differences between fundamental characteristics and factor betas, we compare and contrast the historical returns and risks provided by factors constructed using characteristics and betas. We answer these practical questions: How have portfolios based on these two approaches to constructing factors performed? How should investors use both characteristics and beta information to build higher-performing portfolios?
We show that characteristics are better predictors of stock returns than betas are. Our findings demonstrate that this conclusion generally holds for a wide variety of factors (not only for the most commonly examined) and across international markets. Return predictions alone, however, provide incomplete information. Because investors also wish to measure and manage risks, we examine how the two approaches to factor construction compare in their ability to predict factor risks.
We demonstrate that investors’ objectives inform the practical use of characteristics and betas. An investor who faces few constraints—that is, an investor not bound by tracking error—may use both information sources to create portfolios that earn higher Sharpe ratios than those they could create from either set of factor information alone. Investors may buy or overweight firms with attractive characteristics to attain high returns, and then sell or underweight firms that have similar betas (but unattractive characteristics) to reduce risks. We explain how an investor mindful of tracking error can pursue the same idea, but do so in moderation, thus limiting factor beta exposure relative to a benchmark.
Factors Used in Our Analysis
We analyze a set of factors in the US market over the period July 1963–September 2020 using CRSP/Compustat data.1 The set includes the factors in the Fama and French (2015) five-factor model—market, size, value, profitability, and investment—and the Carhart (1997) momentum factor.
We construct two versions of each factor with the exception of the market factor. The first version is the characteristics-based factor, which is the typical factor constructed by sorting firms into portfolios based on a particular firm characteristic. In this methodology, value firms have a high book-to-market ratio and growth firms have a low book-to-market ratio. The second version is the beta-based factor. Here, we sort firms based on their estimated factor loadings. Value firms are firms with high loadings against the value factor, and growth firms have low loadings. We estimate a firm’s beta using five years of daily stock returns up to month t. Therefore, in our tests, factor return data begin in July 1968. We use the six-factor model to compute the betas of the factors.2
Factor Risk-Adjusted Returns
We look at both average returns and risk-adjusted returns. Returns not adjusted for risk provide an incomplete picture of the relative performance of characteristics- and beta-based factors. Whereas a factor’s return and Sharpe ratio are sufficient to summarize a factor’s performance in the absence of other investments, as part of a broader, real-world portfolio an investor needs to know the factor’s alpha (or information ratio) relative to other portfolio holdings.
Average Returns
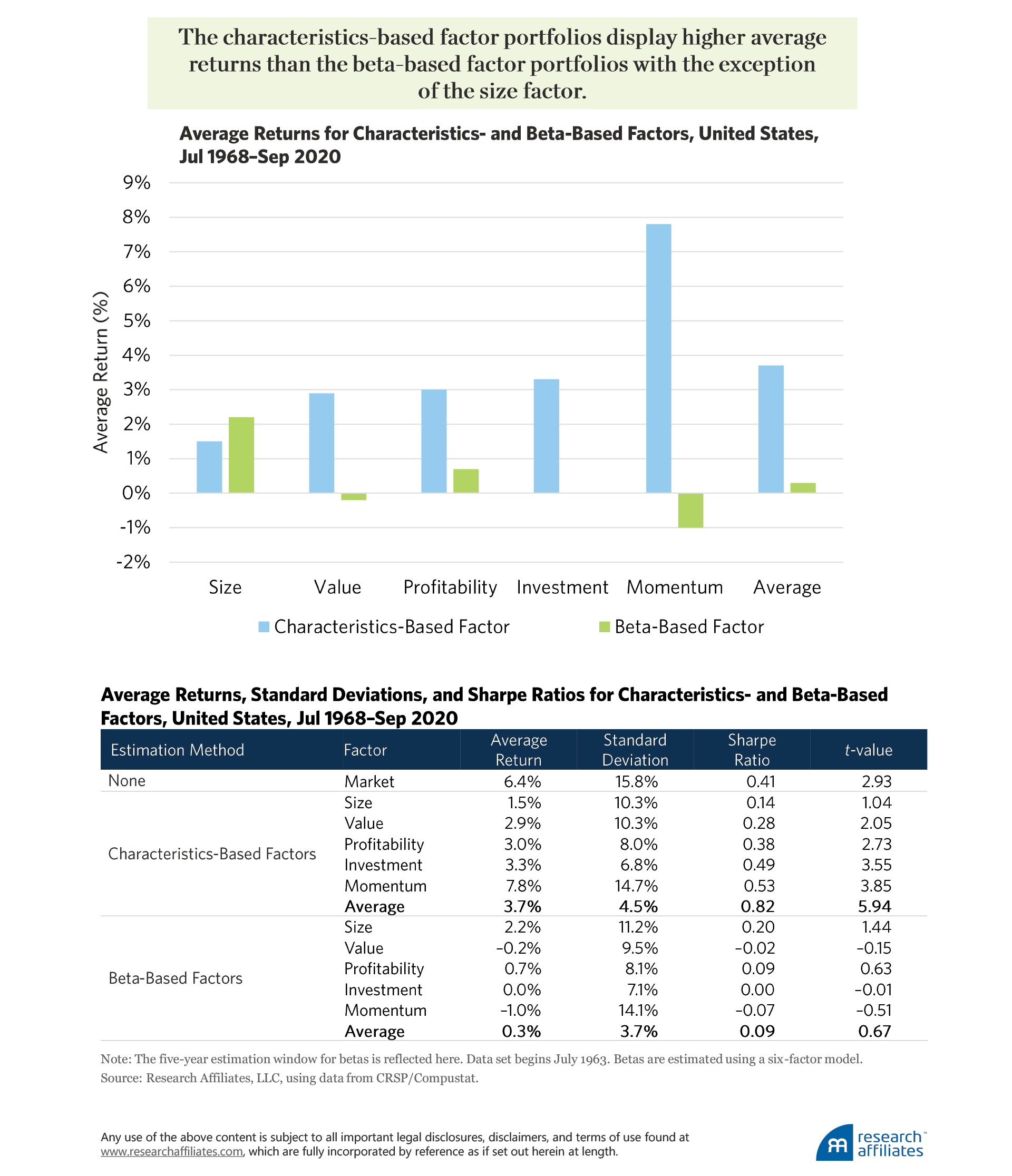
Let’s look first at the average returns unadjusted for risk. We find that the characteristics-based factor portfolios for the Fama-French-Carhart six factors display higher average returns than the beta-based factor portfolios with the exception of the size factor.
Consider, for example, the two value factors. The characteristics-based value factor earns an average return of 2.9% a year and is statistically significant with a t-value of 2.05. The beta-based value factor, by contrast, earns an average return of just −0.2% a year with a t-value of −0.15. Whereas the standard versions of value, profitability, investment, and momentum all earn statistically significant returns at the 5% level, none of the beta-based versions do.
A possible explanation for the similarity in the characteristics- and beta-based metrics for the size factor is the close correlation in firms’ size (SMB) betas with size characteristics, whereas the other factors’ betas do not strongly correlate with their corresponding characteristics. A sort on SMB betas produces portfolios with very similar compositions to the portfolios formed by sorting on firm size.
An equally weighted portfolio of the five characteristics-based nonmarket factors, rebalanced monthly, has a Sharpe ratio of 0.82 (t-value = 5.94) compared to the equally weighted portfolio of beta-based factors, which has a Sharpe ratio of just 0.09 (t-value = 0.67).
Risk-Adjusted Returns
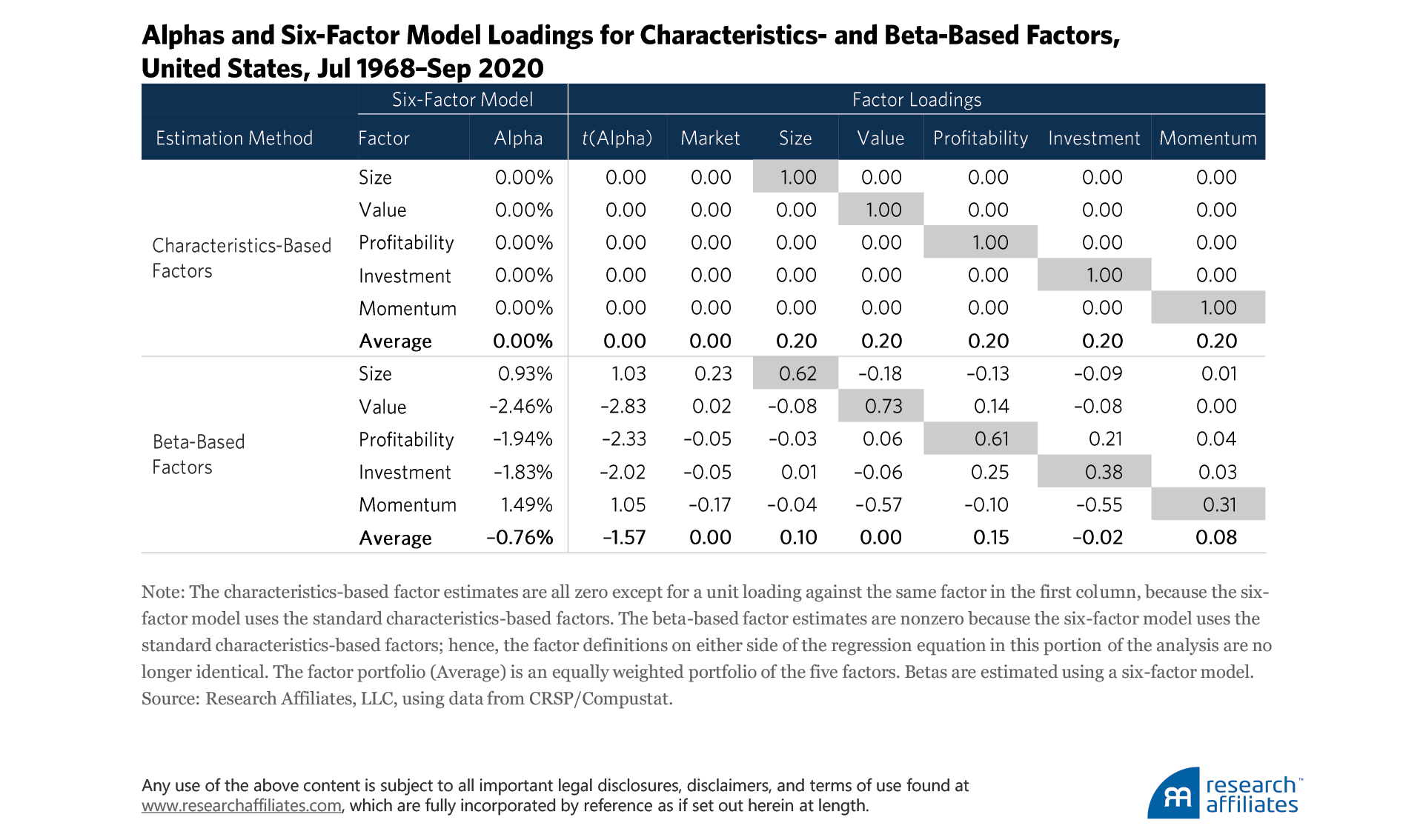
Now, let’s turn our attention to risk-adjusted returns. Although the beta-based factors appear unattractive in terms of their average returns and Sharpe ratios, their loadings against other factors may change an investor’s assessment of their potential to add value in a portfolio. A factor’s low average return, if it has a sufficiently low or even negative correlation with any of the other factors the investor holds, may render it an attractive investment option (Markowitz, 1952).
The estimates of the factor alphas and loadings that we calculate imply that the beta-based factors are valuable from an investment viewpoint. To understand why, it is useful to recall the interpretation of alphas and the t-values associated with these alphas: t-values are proportional to information ratios. If a factor’s alpha is positive and statistically significant in a regression as they are in our calculations, an investor could obtain a significantly higher Sharpe ratio by investing in both versions of the factors (Huberman and Kandel, 1987).
We observe the alpha on, for example, the beta-based value factor (−2.46%) is statistically significantly negative. This indicates that an investor should invest in the factors of the six-factor model and take a short position in the beta-based value factor. Without any additional computations, we already know (from the alpha estimate) that this seven-factor portfolio must earn a higher Sharpe ratio than the portfolio constructed from the six factors alone.
The alphas on three of the beta-based factors—value, profitability, and investment—are statistically significantly negative at the 5% level. What is the intuition for these negative alphas? Although these three beta-based factors earn close-to-zero returns, their positive loadings against the corresponding characteristics-based factors imply they behave very much like the standard characteristics-based factors. Therefore, when we compute the alphas on these factors, the model says these factors should earn almost as high a return as the characteristics-based factor. According to the model, the premium on the beta-based value factor, for example, should be approximately 0.73 × 2.9% = 2.1%. The premium in our calculations, however, is just −0.2%. Therefore, after making the appropriate risk adjustment using the six-factor model, the model leaves these beta-based factors with negative alphas.3
Can Investors Benefit from Beta-Based Factors?
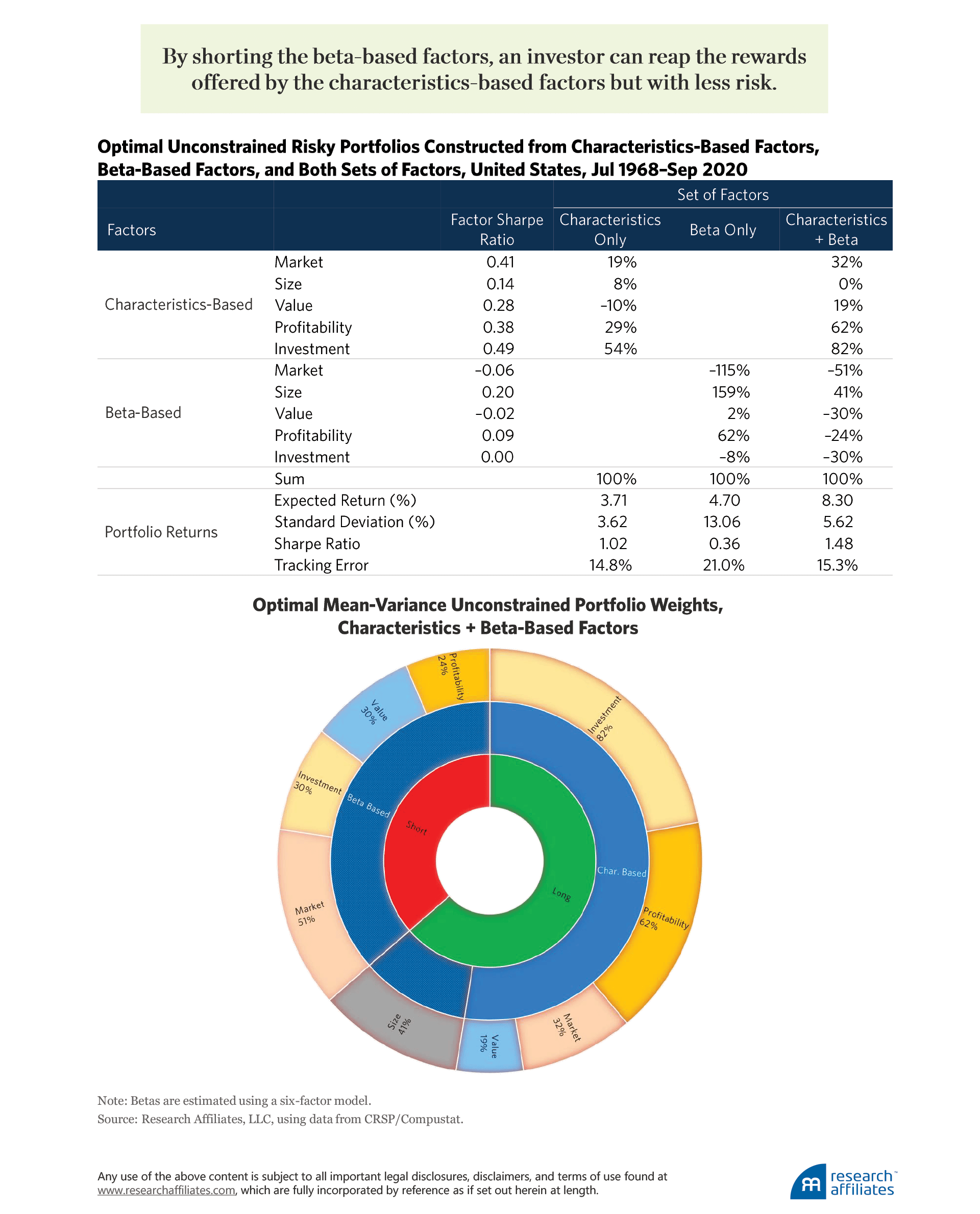
Characteristics- and beta-based factors have exposure to the same risks. For example, when the characteristics-based value factor does poorly, typically the beta-based value factor also performs poorly. This commonality means that an investor holding the characteristics-based factors could use the beta-based factors to manage some of the factor risks. In order to measure the extent to which investors could use the beta-based factors to their benefit, we construct three optimal risky portfolios—characteristics only, betas only, and a combination of the two—and analyze them over the period July 1968–September 2020.
In the first, or characteristics-based, portfolio, an investor who invests in only the five factors in the Fama–French (2015) model would create a portfolio that significantly tilts toward profitability (29%) and investment (54%) and in doing so would earn a Sharpe ratio of 1.02. Note that this Sharpe ratio is an in-sample maximum Sharpe ratio. Because an investor could not have known these factors’ means, variances, and covariances—or perhaps even their identities!—in 1968, this high Sharpe ratio should not be viewed as suggesting investors could have easily outperformed the market in real time (Arnott et al., 2019).
In the second, or beta-based, portfolio, an investor can only earn, at best, a Sharpe ratio of 0.36. This portfolio’s Sharpe ratio is lower than that of the market (0.41) because the beta-based factors, except for the size factor, have low Sharpe ratios. The investor reaches this Sharpe ratio by taking extreme positions in the beta-based size (159%) and market (−115%) factors. The significantly worse Sharpe ratio of the beta-based portfolio compared to the characteristics-based portfolio is unsurprising given our earlier results that betas are poor indicators of the potential for future performance.
In the third, or combined characteristics- and beta-based, portfolio, an investor would find it optimal to construct portfolios using both versions of the factors (except for the size factor), in almost all cases, in the opposite directions! The weights on all characteristics-based factors are positive, while the weights on four of the beta-based factors are negative. By shorting the beta-based factors, an investor can reap the rewards offered by the characteristics-based factors but with less risk. The combination portfolio has a Sharpe ratio of 1.48, a marked increase over the 1.02 Sharpe ratio of the characteristics-based factor portfolio.
Whereas the first and third portfolios have very high Sharpe ratios, investors might be reluctant to invest in them because their tracking errors—defined as the annualized standard deviation of the portfolio’s return minus that of the market—are 14.8% and 15.3%, respectively. These tracking errors for the unconstrained optimal portfolios are very similar to the market’s volatility of 15.8% over our analysis period. Thus, an investor who constructs a portfolio solely by maximizing its Sharpe ratio can create a portfolio entirely disconnected from the market.
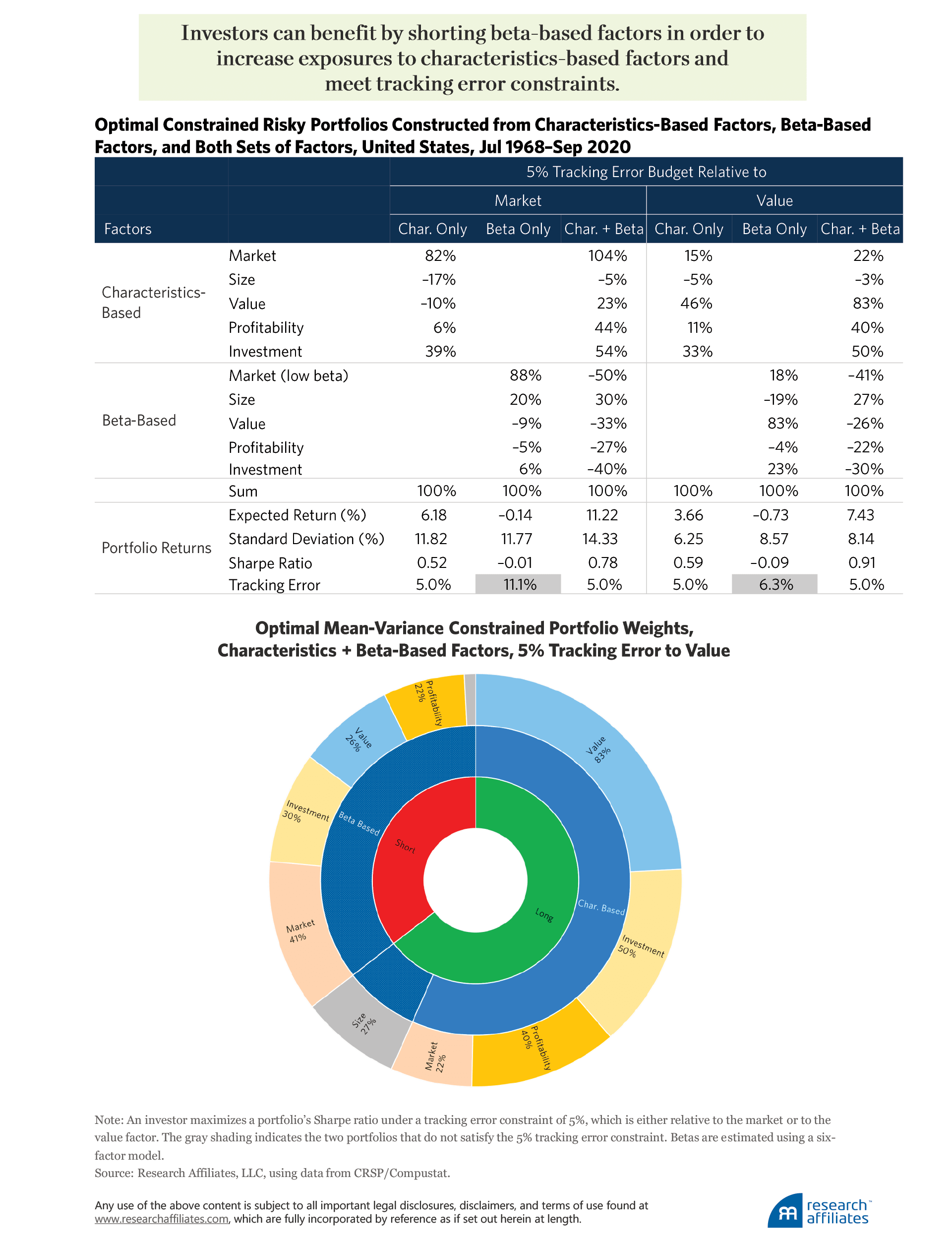
How then would an investor mindful of tracking error solve this investment problem? Let’s consider two investor types. Both investors wish to maximize Sharpe ratios, but to do so in light of a maximum tracking error. One wishes to create a portfolio with a maximum 5% tracking error relative to the market. The other wishes to create a portfolio with a maximum 5% tracking error relative to the value index (here, the typical characteristics-based long–short value factor).
The first investor could satisfy the tracking error constraint by holding only the market factor and the second investor by holding only the value factor. Because the investors are willing to assume up to a 5% tracking error, however, they can seek to increase their portfolios’ Sharpe ratios by also investing in other factors.
In order to maximize the Sharpe ratio, we construct portfolios for each of the investors using characteristics only, betas only, and a combination of the two. Neither of the portfolios constructed using the beta-based factors meets the investors’ 5% tracking error constraints at 11.1% (versus the market) and 6.3% (versus the value index).
The two optimal constrained portfolios constructed using a combination of characteristics- and beta-based factors, however, meaningfully benefit investors. By shorting four of the beta-based factors, investors are able to increase their exposures to the characteristics-based factors, meet their tracking error constraints, and earn Sharpe ratios of 0.78 (versus the market) and 0.91 (versus the value index).
We have shown that beta-based factors can benefit both constrained and unconstrained investors. The benefit is consistent with how the two types of metrics—characteristics and betas—forecast future returns and risks. Investors cannot earn higher risk-adjusted returns by tilting toward beta-based factors, but they can benefit by using them to hedge risks.
Investors can employ characteristics-based factors more aggressively in their portfolios in conjunction with beta-based factors to keep portfolio risks at manageable levels. The extent to which an investor should use beta-based factors in a portfolio depends on their objectives—the less constrained an investor, the more benefits the beta-based factors can yield.
Conclusions
We show that fundamental factor characteristics provide superior information about portfolio returns compared to factor betas. Portfolios with high exposure to factor betas but little exposure to factor characteristics earn average returns that are not statistically or economically different from zero. We demonstrate that this result holds for the six most commonly used factors, and as discussed by Brightman et al. (2021), across an even wider array of factors and across international markets.
We also show that factor betas provide information useful in managing risk. By buying or overweighting characteristics-based factor exposures and selling or underweighting beta-based factor exposures, investors may reap the rewards of factor investing while bearing less risk. Choosing factor-investing strategies to maximize factor betas may provide factor risks without the desired returns. Characteristics-based factor analytics provide better information about factor-based investment strategies’ prospects for delivering factor returns.
Please read our disclosures concurrent with this publication: https://www.researchaffiliates.com/legal/disclosures#investment-adviser-disclosure-and-disclaimers.
Endnotes
- Brightman et al. (2021), on which this article is based, also study a second set of factors containing nine slightly less popular factors: short-term reversals, long-term reversals, idiosyncratic volatility, Amihud’s illiquidity, low beta, earnings-to-price ratio, cash flow-to-price ratio, accruals, and net share issues. In addition to the US market, both factor sets were studied in three international markets—Europe, Asia excluding Japan, and Japan—over the period January 1988–September 2020. The results of the analysis for both factor sets across the three international markets supports the authors’ findings in the US market, as reported in this article.
- Please refer to Brightman et al. (2021) for details on the factor construction methodology used in this analysis.
- Brightman et al. (2021) estimate cross-sectional Fama–MacBeth regressions for the July 1968–September 2020 period using two sets of predictors for the US stock market: characteristics and betas. They find that stock characteristics are predictive of subsequent returns, but that estimated betas do not have predictive power. They also find that historical betas (with the exception of investment and momentum betas) are approximately as predictive of future betas as current stock characteristics. For full details of the cross-sectional analysis we refer you to Brightman et al.
References
Arnott, Robert, Campbell Harvey, Vitali Kalesnik, and Juhani Linnainmaa. 2019. “Alice’s Adventures in Factorland: Three Blunders that Plague Factor Investing.” Journal of Portfolio Management, vol. 45, no. 4:18–36.
Brightman, Chris, Forrest Henslee, Vitali Kalesnik, Feifei Li, and Juhani Linnainmaa. 2021. “Why Are High Factor Exposures to Factor Betas Unlikely to Deliver Anticipated Returns?” Available on SSRN.
Carhart, Mark. 1997. “On Persistence in Mutual Fund Performance.” Journal of Finance, vol. 52, no. 1:57–82.
Fama, Eugene, and Kenneth French. 2015. “A Five-Factor Asset Pricing Model.” Journal of Financial Economics, vol. 116, no. 1:1–22.
Huberman, Gur, and Shmuel Kandel. 1987. “Mean-Variance Spanning.” Journal of Finance, vol. 42, no. 4 (September):873–888.
Markowitz, Harry. 1952. “Portfolio Selection.” Journal of Finance, vol. 7, no. 1:77–91.