
Conventional risk measures may not accurately describe the volatility investors actually experience, especially for portfolios servicing their retirement spending needs.
Return volatility rises as its calculated holding period nears 1 year and falls as it lengthens to 10 years. Lower volatility at longer holding periods implies that longer-term mean reversion exists.
A portfolio achieves the greatest extra-return benefit by rebalancing over the holding period of highest volatility.
Time diversification is helpful, up until long-term uncertainty about the value of reinvested cash flows from dividends leads to rising volatility.
‘Tis all men’s office to speak patience
To those that wring under the load of sorrow,
But no man’s virtue nor sufficiency
To be so moral when he shall endure
The like himself.
—William Shakespeare, Much Ado About Nothing (1598–99), Act V, scene 1, line 27.
Investing is traditionally billed as a trade-off between the return and risk of a portfolio. The definition of return—the portfolio wealth gained or lost—is relatively straightforward. But the multitude of quantitative risk measures available to investors today can make the definition of investment risk mysterious and complex.
A conventional way of defining an investment’s absolute risk is its volatility, or standard deviation of returns. Industry standard practice is to calculate this metric using short-term holding period returns. Monthly—and increasingly daily—horizons are being used by the dominant global investment data analytics providers, such as Bloomberg, Morningstar, and eVestment Alliance.
But does this conventional, seemingly simple risk measure, calculated using very short-term data periods, accurately describe the volatility investors experience, many of whom have much longer horizons, such as for retirement planning, over which they bear risk?
We find that the length of holding period we use to assess risk has profound implications for the true level of volatility that investors face in their portfolios. Our analysis also suggests the optimal horizon for rebalancing a portfolio and for determining the period over which we can more accurately predict returns. Before blindly accepting a stated proxy of risk, we owe it to ourselves to understand how risk, as defined by the standard deviation of returns, differs over various time horizons—and importantly, why it matters.
The Relationship between Holding Period and Risk
The research and practitioner community has had a long fascination with the estimation of short-term volatility. While the technicalities of this undertaking are enthralling for the mathematically inclined, such an undertaking is beyond the scope of this article.1 Instead, we focus on a much humbler goal of analyzing how the characteristics of historical return volatility vary over different holding-period lengths. Our analysis suggests that the basic rule investors use to estimate the most rudimentary measure of portfolio risk, annual volatility, is misleading.
Annualized return volatility, or the annualized standard deviation of returns measured on a rolling t-year period, is most commonly calculated using the following formula, where r is defined as returns over a holding period of t years:
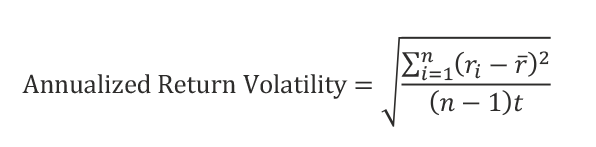
From a naïve statistical perspective, the larger the number of observations, the more accurate our measurement of volatility. As such, unsurprisingly, the standard industry practice is to calculate volatility using very short-term holding period returns, such as monthly or even daily periods. While this simplifying approach, necessary in all modeling, is required to yield tractable solutions, it behooves us to recognize the danger of drawing incorrect inferences from assumptions that are overly simplistic and can prove to be obviously misleading!
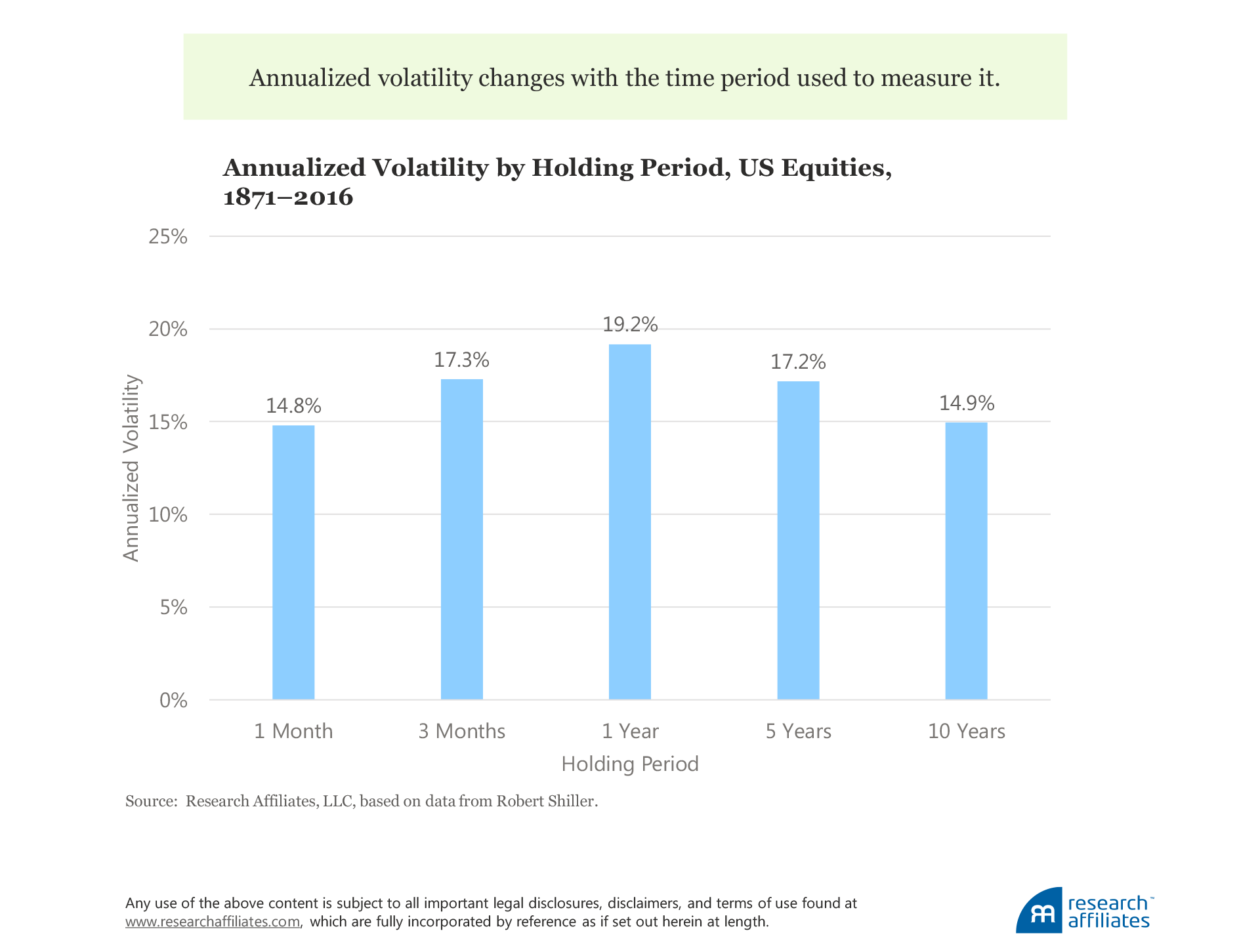
If the time series of an investment’s monthly return is unrelated from month to month, then per theory, its annualized volatility should be the same, regardless of the holding period. Yet, when we examine the full history of US equities, this simply doesn’t hold. We calculate the annualized volatility of US equities from 1871 to 2016, measured over holding periods from one month to 10 years. Over the full time span, the annualized volatility of US equities calculated using monthly return data is 14.8%. As the horizon increases, this measure of risk rises, approaching a peak of 19.2% when based on annual return data. For holding periods beyond 1 year, the annualized volatility declines, falling back to 14.9% when calculated using a 10-year holding period.
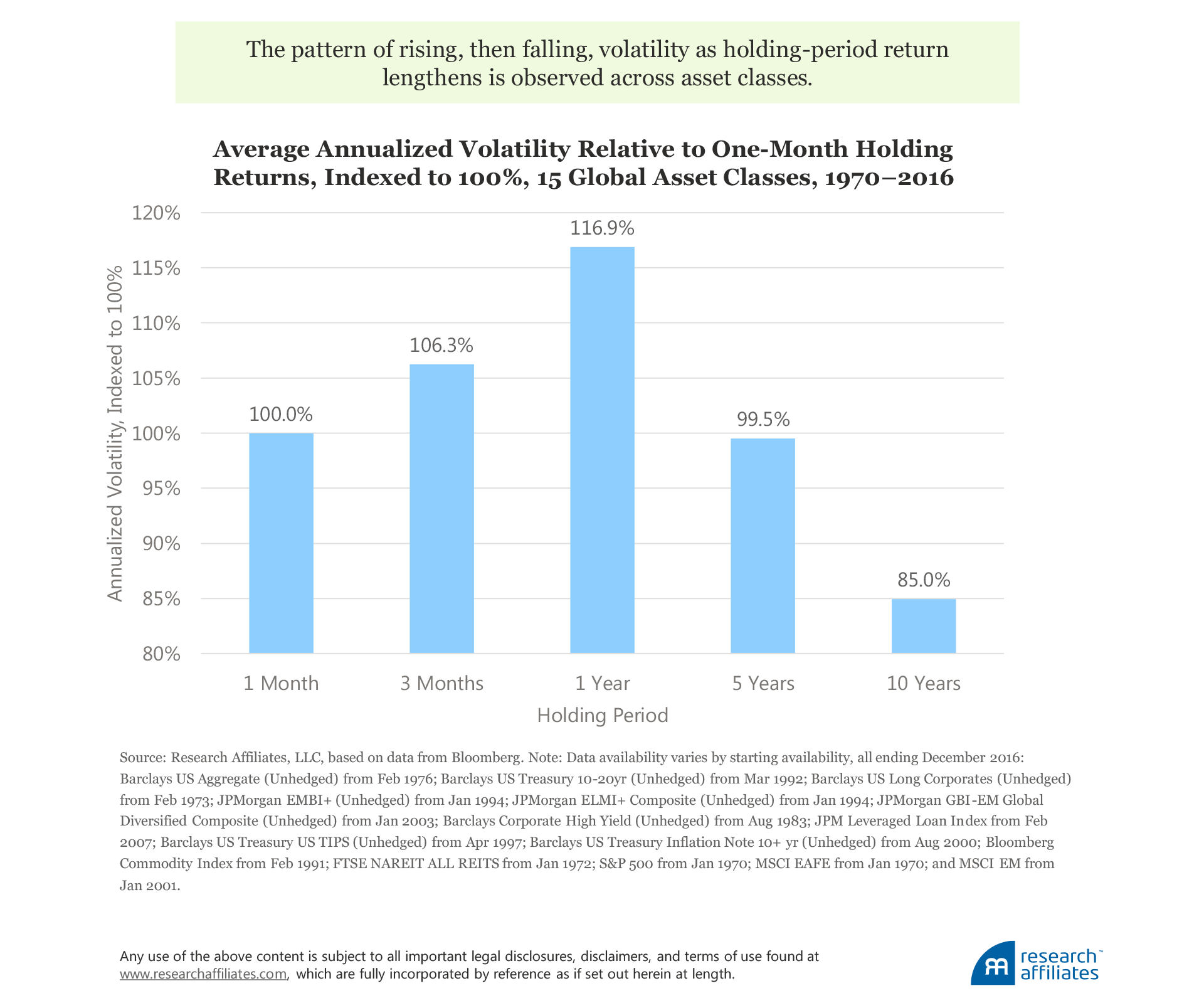
We extend our analysis to 15 global asset classes to determine if our results are unique to US stocks, or if they apply more broadly. Each of the 15 global asset classes has a long-run annualized volatility greater than 5%. We evaluate the annualized volatility as a percentage of the traditional one-month calculation.2 For the subperiod 1970–2016, the behavior of volatility, on average, across the asset classes that we study, reflects a consistent pattern as the length of holding period rises. Again, we see that the monthly returns of a wide range of asset classes are not independent through time, but that annualized volatility varies depending on the holding period used to calculate the risk measure.
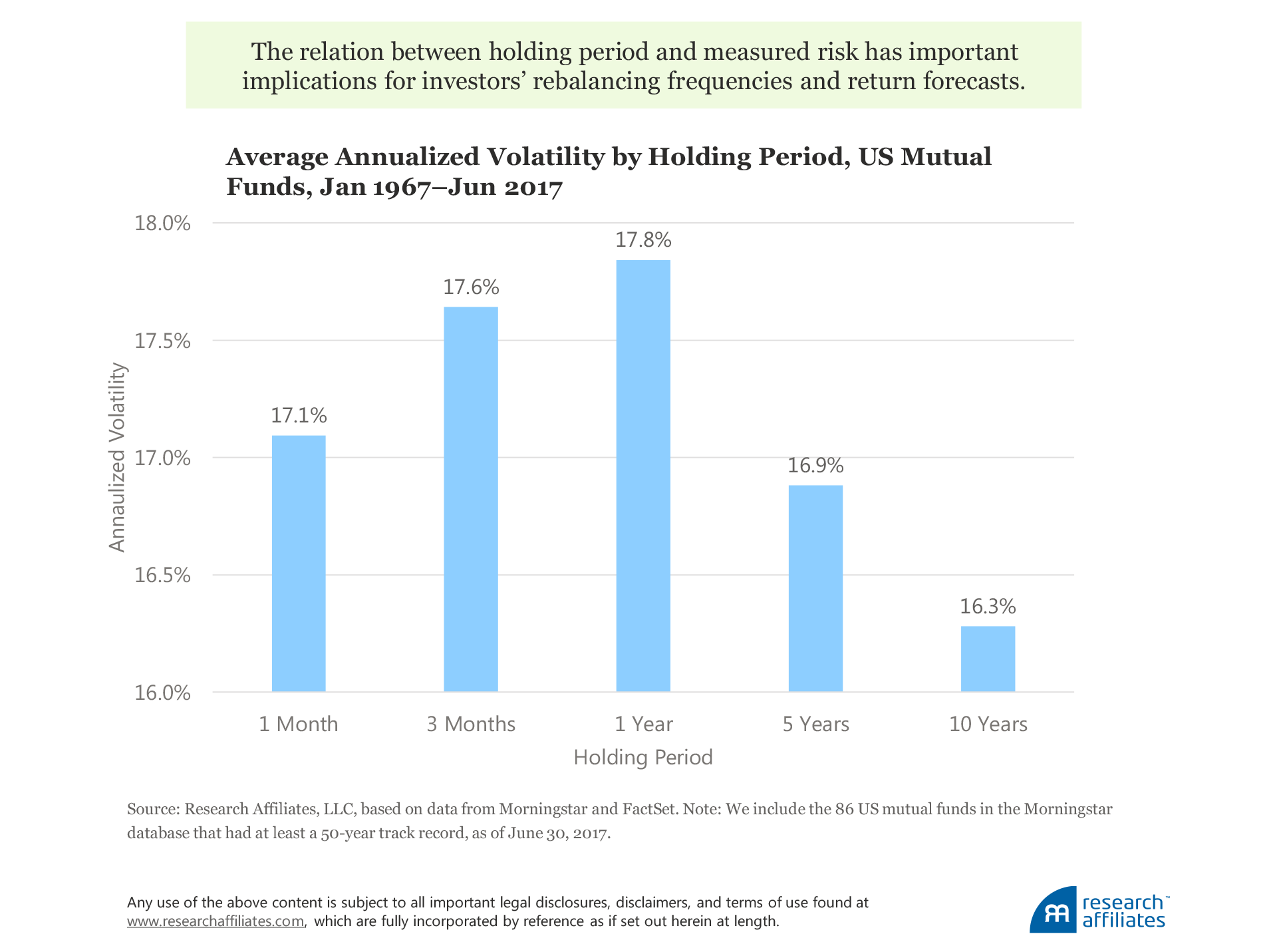
We also repeat this exercise across 86 US mutual funds in the Morningstar database. Each mutual fund we include had at least a 50-year track record, as of June 30, 2017. Once again, a familiar pattern arises. The average return volatility of these longest-surviving mutual funds increases as the holding period used in the calculation approaches 1 year, and then declines as the holding period lengthens to a 10-year interval. This finding matters to investors and to investment outcomes. Before we explain why it matters, let’s first examine why the observed annualized volatility pattern exists.
Why Volatility Changes with the Holding Period
Time diversification refers to the notion that time diversifies risk, implying that the volatility of risky assets falls over long periods of time. This characteristic is based on the independence of returns. Obviously, the simplified independence assumption does not hold, and in no way are we suggesting this is a novel insight. The impact of time diversification on portfolio risk has been a running debate for decades,3 with several prominent financial economists arguing on both sides, most recently Kritzman (2015). A key element in this discussion is an investor’s view on the behavior of financial markets, namely, the existence and strength of short-term continuation and of long-term reversion.4
The existence of rising holding-period volatility when moving from monthly to annual holding periods is well accepted, given the presence of positive, albeit weak, correlation between monthly returns. In the finance realm, we know this as momentum. A comprehensive set of research has been undertaken on this persistent phenomenon, including work by Moskowitz, Ooi, and Pedersen (2012), who find “time series momentum in virtually every instrument we examine.” We (Aked, Mazzoleni, and Shakernia [2016]) recently contributed to the discussion, relating the equity return momentum to the persistence of macroeconomic cycles; our work is based on the research of Adam, Marcet, and Nicolini (2016).
More academically controversial is the acceptance of mean reversion, or negative correlation, in returns over longer periods of time. The challenge lies in quantitatively proving that it does, because longer holding periods necessarily result in much smaller independent datasets, which leads to statistical problems. As such, the question of whether mean reversion exists becomes a philosophical issue with many believing in,5 and others categorically denying, its existence.
Despite the inherent challenges of generating statistical proof, we posit that long-term mean reversion exists in returns, driven at least, but not exclusively, by the reinvestment of distributions. Recall that a decline in measured annualized return volatility over longer holding periods implies and requires longer-term mean reversion to exist.
We submit that academia’s preoccupation with statistical significance should not keep us from investigating long-term holding-period volatility assumptions. Consider the story of the man who looks under a lamppost for keys he lost on the other side of the street—because under the lamppost is where the light is!6 Further analyzing the already-illuminated area of short-term risk is easy, but doing so precludes our learning about the time periods that matter most for investors.
To shed more light on the issue, we create a theoretical equity index investment with a fixed and known dividend. Over short-term horizons, both its dividend cash flows and its capital price changes drive its returns. Unsurprisingly, the volatilities of its total returns and of its price returns are very similar, because the volatility of its dividend cash flows is low relative to the volatility of its capital price changes.
Moving through time, over a period from a decade to a quarter-century, the path of capital prices will lead to larger or smaller capital allocations from reinvested dividends. These two forces, the capital price and the capital accumulation from reinvested dividends, offset each other and lower investment risk; in other words, share prices and capital accumulation due to reinvested cash flows are inherently negatively correlated.7 Eventually, the impact of the initial investment on its future return becomes much less important, and the predominant influence on the investment’s expected return comes from the path of future unknown reinvestment prices.
After undertaking the math, we plot the expected shape of the investment volatility for this theoretical asset. As expected, we observe that investment volatility declines from the annual holding period until it reaches its lowest point, which interestingly occurs when the holding period is approximately one-and-a-half times the ratio of price to cash flow. For example, if a cash-flow yield is 5% (equivalently, a price-to-cash-flow ratio of 20 times), the holding period of lowest volatility is around 30 years.8
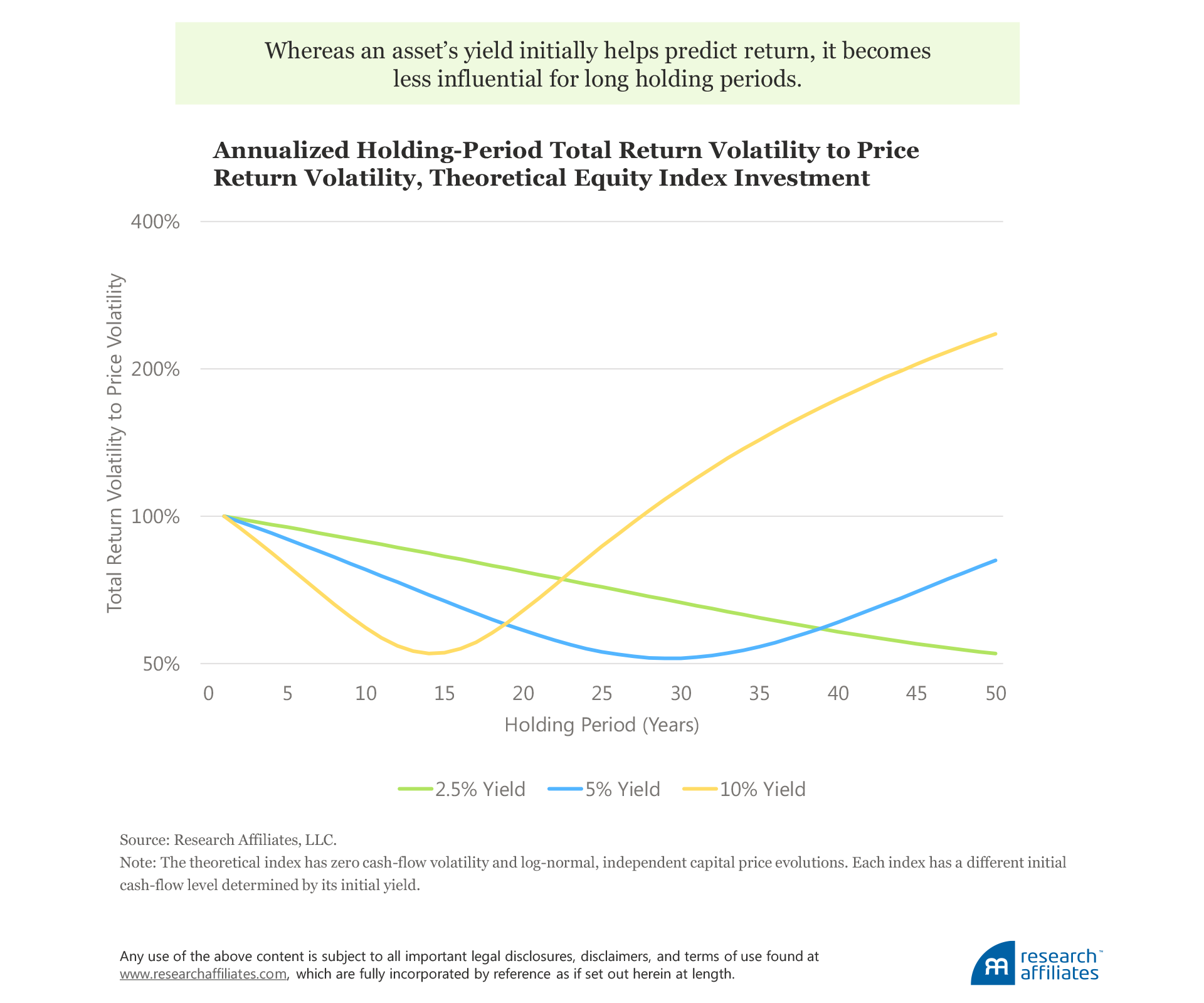
We must highlight that our model provides a guide to the characteristic of holding-period volatility for perpetual assets. In reality, our assumptions that cash flows have zero volatility and that prices do not have any continuation or reversion characteristics are not defendable. That said, the characteristic of initially falling, then rising, annualized volatility in the very long term is instructive and should influence how investors manage their portfolios. We simply posit that—even for those who do not believe in the long-term reversion of asset prices—an asset having larger price volatility than cash-flow volatility demonstrates significant total-return reversion.
Beyond the threshold of minimum volatility and the uncertainty of the value of reinvested dividends, the historical price volatility of an asset increases substantially. Revisiting the time diversification discussion, we can credit points to supporters of both sides of the argument: time diversification is helpful—at least up to the point in time when long-term uncertainty about the value of reinvested cash flows from dividends begins to lead to rising volatility. Simply, the longer the investment horizon, more is subject to unknown forces. Who could possibly know what market environment investors will face far out in the future? At very long horizons, uncertainty dominates and volatility rises, and we, as investors, become pawns in the game of the market.
So Why Does All This Matter?
Having made the case that volatility does change with the time period used to measure it, we would like to explain why this matters, or should matter, to investors.
First, it behooves us as investors to understand which volatility measure will be the most accurate predictor of risk in our portfolios. The frequently reported volatility measure based on monthly or daily returns is useful if we care about understanding how our monthly or daily returns may vary. If, instead, we want to understand the volatility of a portfolio that could service our retirement spending needs, then we ought to consider risk measures with the characteristics of long holding periods. We encourage investors to search beyond the light of the lamppost where the data are less easily found.
On a similar note, although our article focuses solely on one definition of absolute risk, the standard deviation of returns, we encourage investors to adopt a balanced view of risk by considering various risk metrics. Importantly, let’s not forget the role of maverick risk in investment decisions and investment errors (Arnott, 2003).
Second, the relationship between risk and holding period can help inform other critical decisions, such as determining at what frequency investors should rebalance their portfolios. Research suggests that a portfolio of diversified assets gains additional return from diversification itself.9 Interestingly, the level of extra return gained from the “diversification benefit” depends on asset-class volatility, which implies that a portfolio will achieve the greatest extra-return benefit by rebalancing over the holding period of highest volatility. Because the highest volatility seems to consistently occur when the holding period approaches one year, which also happens to be the time period separating continuation and reversion of asset returns, our analysis provides additional support to the ongoing debate related to the frequency of rebalancing.
Additionally, we find that for most asset classes, the volatility of the total return declines when holding periods are measured in decades, making it easier to predict returns when measured volatility is at its lowest. This suggests that for most asset classes, it is optimal to predict returns over a long time frame—up to an extent!
Estimating the wealth of an investment portfolio over an extremely long horizon is futile, because over the very long run, the compounded value of reinvested dividends or required distributions will depend on a myriad of possible paths of capital prices, which creates an uncomfortably massive range of possible wealth outcomes.
Whereas our fast-paced, performance-obsessed world taunts us to assess our portfolios over very short horizons, most investors actually have a sufficiently long horizon to enjoy the benefits of time diversification.10 While we may logically understand and appreciate this, do we exhibit the patience and courage to hold the course when experiencing the inevitable bouts of short-term pain and disappointment?
To better tolerate the discomfort of uncertainty, perhaps it’s best to heed the timeless advice offered by the likes of Shakespeare and Leonardo da Vinci. As the latter aptly said 500 years ago:
Patience serves as a protection against wrongs, as clothes do against cold. For if you put on more clothes as the cold increases, it will have no power to hurt you. So in like manner you must grow in patience when you meet with great wrongs, and they will be powerless to vex your mind.
Appendix
In the simplest approach, we assume that a fixed annual cash flow per share, y, is used to buy additional shares, h. In this case, we can calculate the annualized holding period return of this investment as
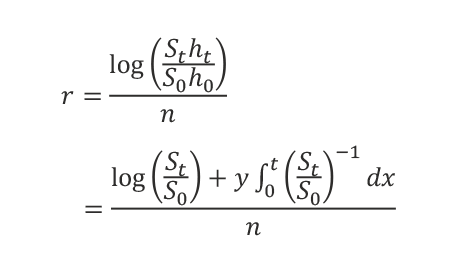
Simply, in the short term, a falling price allows us to buy more shares with our cash flow. Alternatively, a rising price leads to a smaller increment in share ownership. This negative relationship between price, S, and shares, h, means that the return naturally becomes negatively correlated across longer time periods. The ratio of the return variance for holding period n, 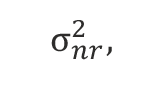 to the capital price variance,
to the capital price variance, 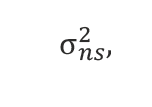 can be approximated as the following relationship:
can be approximated as the following relationship:
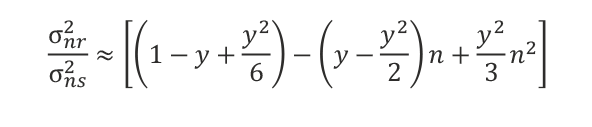
Endnotes
1. We refer interested readers to Poon and Granger (2003) for a comprehensive paper that reviews a broad range of volatility models and includes a reference list approaching 200 articles.
2. For example, if the annualized volatility of the asset class is 10% (using monthly data) and 12% (using annual data), we index the annual holding-period volatility as 120% of the monthly holding-period volatility.
3. Butler and Domian (1991) is an early contribution to the decades-long debate on time diversification and portfolio risk.
4. Continuation, or momentum, is just positive autocorrelation of returns; likewise, mean reversion, or value, is negative autocorrelation of returns.
5. The central philosophy of Research Affiliates is that the largest and most persistent active investment opportunity arises from long-horizon mean reversion (Brightman, Treussard, and Masturzo [2014]).
6. This story, which comes in a few versions, represents the concept of the “streetlight problem,” a type of bias that arises when people (e.g., statisticians or economists) search for something where the search is easiest.
7. In the short term, falling prices allow us to buy more shares with our cash flow. Alternatively, rising prices lead to a smaller increment in share ownership. This negative relationship between prices and shares means that the returns naturally become negatively correlated across longer time periods. Please refer to the appendix for mathematical proof.
8. Our simplified model implies that the minimum annualized volatility will occur in year, 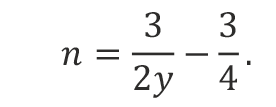 We can say this is 1.5× the price-to-cash flow ratio. Although we haven’t included the algebra, it can be verified by determining the turning point of our relative volatility equation presented in the appendix.
We can say this is 1.5× the price-to-cash flow ratio. Although we haven’t included the algebra, it can be verified by determining the turning point of our relative volatility equation presented in the appendix.
9. See Willenbrock (2011) for a discussion of the diversification return, which does not require rebalancing as shown by Cuthbertson et al. (2016) unless annualized holding-period volatilities are different, which our assertion demonstrates.
10. According to a 2015 study by Willis Towers Watson (McFarland, 2016), the average duration of pension plan obligations of more than 400 Fortune 1000 companies was approximately 13 years. Among defined contribution plans, for which lifecycle/target date funds are among the most popular investment vehicles, over 70% of all lifecycle/target date assets are invested in vintages of 2025 or later, with the largest amount of assets in the 2030 vintage (15-year horizon).
References
Adam, Klaus, Albert Marcet, and Juan Pablo Nicolini. 2016. “Stock Market Volatility and Learning.” Journal of Finance, vol. 71, no. 1 (February):33–82.
Aked, Michael, Michele Mazzoleni, and Omid Shakernia. 2016. “When a Storm Is in the Offing: Fundamental Growth in the U.S. Equity Market.” Research Affiliates (June).
Arnott, Robert. 2003. “What Risk Matters? A Call for Papers!” Financial Analysts Journal Editor’s Corner, vol. 59, no. 3 (May/June):6–8.
Brightman, Chris, Jonathan Treussard, and Jim Masturzo. 2014. “Our Investment Beliefs.” Research Affiliates (October).
Butler, Kirt, and Dale Domian. 1991. “Risk, Diversification, and the Investment Horizon.” Journal of Portfolio Management, vol. 17, no. 3 (Spring):41–47.
Cuthbertson, Keith, Simon Hayley, Nick Motson, and Dirk Nitzsche. 2016. “Diversification Returns, Rebalancing Returns and Volatility Pumping.” Working paper (February). Available at SSRN.
Kritzman, Mark. 2015. “What Practitioners Need to Know... About Time Diversification (corrected).” Financial Analysts Journal, vol. 71, no. 1 (January/February):29–34. Reprinted from Financial Analysts Journal, vol. 50, no. 1 (January/February 1994):14–18.
McFarland, Brendan. 2016. “A Continuing Shift in Retirement Offerings in the Fortune 500.” Willis Towers Watson (February 18).
Moskowitz, Tobias, Yao Hua Ooi, and Lasse Pedersen. 2012. “Time Series Momentum.” Journal of Financial Economics, vol. 104, no. 2 (May):228–250.
Poon, Ser-Huang, and Clive Granger. 2003. “Forecasting Volatility in Financial Markets: A Review.” Journal of Economic Literature, vol. 41, no. 2 (June):478–539.
Willenbrock, Scott. 2011. “Diversification Return, Portfolio Rebalancing, and the Commodity Return Puzzle.” Financial Analysts Journal, vol. 67, no. 4 (July/August):42–49.
